
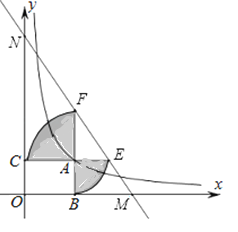
【题目】如图,已知动点A在函数![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
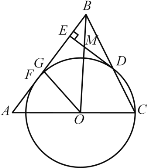
【题目】如图,在△ABC中,AB=AC=10,tan∠A=![]() ,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
(1)求证:DE是⊙O的切线;
(2)当⊙O与AB相切于点F时,求⊙O的半径;
(3)在(2)的条件下,连接OB交DE于点M,点G在线段EF上,连接GO.若∠GOM=45°,求DM和FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某体育看台侧面的示意图,观众区AC的坡度i=1:2,顶端C离水平地面AB的高度为15m,顶棚外沿处的点E恰好在点A的正上方,从D处看E处的仰角α=30°,竖直的立杆上C,D两点间的距离为5m.
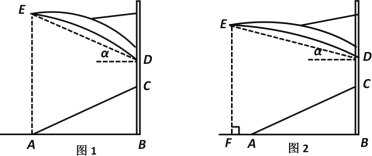
(1)求观众区的水平宽度AB.
(2)求图1中点E离水平地面的高度EA.
(3)因为遮阳需要,现将顶棚ED绕D点逆时针转动11°30′,若E点在地面上的铅直投影是点F(图2),求AF.(sin11°30′≈0.20,cos11°30′≈0.98,tan11°30′≈0.20;sin18°30′≈0.32,cos18°30′≈0.95,tan18°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
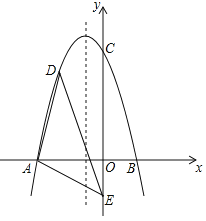
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,若将50件该商品按标价打八折销售,比按原标价销售这些商品少获利200元.
![]() 求该商品的标价为多少元;
求该商品的标价为多少元;
![]() 已知该商品的进价为每件12元,根据市场调査:若按
已知该商品的进价为每件12元,根据市场调査:若按![]() 中标价销售,该商场每天销售100件;每涨1元,每天要少卖5件
中标价销售,该商场每天销售100件;每涨1元,每天要少卖5件![]() 那么涨价后要使该商品每天的销售利润最大,应将销售价格定为每件多少元?最大利润是多少?
那么涨价后要使该商品每天的销售利润最大,应将销售价格定为每件多少元?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②2a+b=0;③3a+c>0;④4a﹣2b+c<0:⑤9a+3b+c<0.其中结论正确的个数有( )
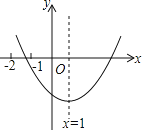
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
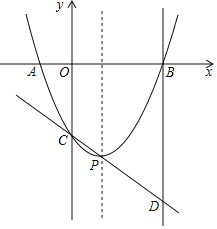
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,顶点为P,直线
轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,顶点为P,直线![]() 与过点B且垂直于
与过点B且垂直于![]() 轴的直线交于点D,且CP:PD=1:2,tan∠PDB=
轴的直线交于点D,且CP:PD=1:2,tan∠PDB=![]() .
.
(1)请直接写出A、B两点的坐标:A , B ;
(2)求这个二次函数的解析式;
(3)在抛物线的对称轴上找一点M使|MC-MB|的值最大,则点M的坐标为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com