
|
|
| m |
| 0.1 |
| m |
| 0.1 |


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
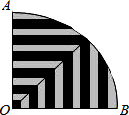 将如图所示的圆心角为90°的扇形条纹纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),OA=OB=8,则围成的圆锥形纸帽的高是
将如图所示的圆心角为90°的扇形条纹纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),OA=OB=8,则围成的圆锥形纸帽的高是查看答案和解析>>
科目:初中数学 来源: 题型:
 已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点.
已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲 | 乙 | |
| 进价(元/件) | 15 | 20 |
| 售价(元/件) | 17 | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com