
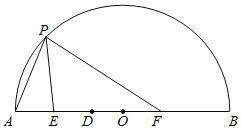
����Ŀ����ͼ��D��ֱ��AB��һ���㣬E��F�ֱ���AD��BD���е㣬P��![]() ��һ���㣬����PA��PE��PF����֪AB��6cm����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy1cm��P��F�����ľ���Ϊy2cm��
��һ���㣬����PA��PE��PF����֪AB��6cm����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy1cm��P��F�����ľ���Ϊy2cm��
С�ڸ���ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С�ڵ�̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0.97 | 1.27 | �� �� | 2.66 | 3.43 | 4.22 | 5.02 |
y2/cm | 3.97 | 3.93 | 3.80 | 3.58 | 3.25 | 2.76 | 2.02 |
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2��������������y1��y2��ͼ��
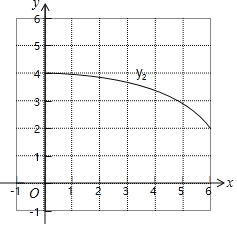
��3����Ϻ���ͼ������⣺����PEFΪ����������ʱ��AP�ij���ԼΪ�� ��cm��
���𰸡���1��1.90����2������������3��3.5��3.8��4.8
��������
��1��ͨ����ͼ�������ɵñ��е�������ֵ��
��2���ѱ���������赽ƽ��ֱ������ϵ�У�����ƽ�����������Ӽ��ɻ�������y1��y2��ͼ��
��3����Ϻ���ͼ���ɵõ���PEFΪ����������ʱ��AP�ij��ȣ�
��1��ͨ��������֪��
���е�������ֵ��1.90��
�ʴ�Ϊ��1.90��
��2������y1��y2��ͼ����ͼ��

��3���۲�ͼ���֪��
��PEFΪ���������Σ��ٵ�PE=PFʱ��![]() ���������Ľ��㣬AP�ij���ԼΪ3.8 cm���ڵ�PE=EFʱ��
���������Ľ��㣬AP�ij���ԼΪ3.8 cm���ڵ�PE=EFʱ��![]() ��AP�ij���ԼΪ3.5cm���۵�PF=EFʱ��
��AP�ij���ԼΪ3.5cm���۵�PF=EFʱ��![]() ��AP�ij���ԼΪ4.8 cm��
��AP�ij���ԼΪ4.8 cm��
�ʴ�Ϊ��3.5��3.8��4.8��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������м���:�������Ϻ�����,��ʵ����,���º�ʮ��.�º����,��ʵһ��,���Ϻ̶���.���ϡ��º�ʵһ��������?���������:�����ϵȵ�������,��������Ĺ����ټ�����,���൱��ʮ���µȵ��Ӵ�����Ĺ���.���µȵ�������,��������Ĺ����ټ�һ��,���൱�������ϵȵ��Ӵ�����Ĺ���.���ϵȡ��µȵ���ÿ���ܴ���ٶ�����?���ϵȵ���ÿ���ܴ�x������,�µȵ���ÿ���ܴ�y������,��������,���з�����Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������������ҩ��ʹҩ���������ڷ�����Ч���ã���ҩ���ѪҩŨ��Ӧ���������ЧŨ��������ж�Ũ��֮�䣮ij���˻����ڵ��οڷ�1��λijҩ������ѪҩŨ�ȼ������Ϣ��ͼ��
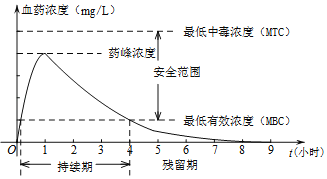
����ͼ���ṩ����Ϣ�����й��ڳ��˻���ʹ�ø�ҩ���˵���У�
���״η��ø�ҩ��1��λԼ10���Ӻ�ҩ�����Ч���ã�
��ÿ���4Сʱ���ø�ҩ��1��λ������ʹҩ����������������ã�
��ÿ�η��ø�ҩ��1��λ�����η�ҩ���С��2.5Сʱ�����ᷢ��ҩ���ж���
������ȷ��˵����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
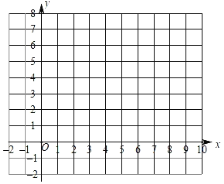
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��x��5��ֱ��y��3��x��ֱ��ڵ�A��B��ֱ��y��kx+b��k��0��������A����x�ύ�ڵ�C��9��0����
��1����ֱ��y��kx+b�ı���ʽ��
��2���ᡢ�����궼�������ĵ�������㣮���߶�AB��BC��CAΧ�ɵ��������߽磩ΪW��
�ٽ�Ϻ���ͼ��ֱ��д������W�ڵ����������
�ڽ�ֱ��y��kx+b����ƽ��n����λ����ƽ�ƺ��ֱ��������Wû�й�����ʱ������ͼ��ֱ��д��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
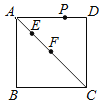
����Ŀ����ͼ����������ABCD�У�AB��4��E��F�ǶԽ���AC�ϵ��������㣬��EF��2��P���������ı��ϵ�����һ�㣮����PEF�ǵȱ������Σ������������P�㹲��_____������ʱAE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�AB��CD��EF��GH��������OPQR���ϵ��߶Σ���M������ij���߶��ϣ�������OM��x��������ļн�Ϊ������sin����cos�������M���ڵ��߶ο����ǣ�������
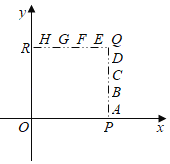
A.AB��CDB.AB��EFC.CD��GHD.EF��GH
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=x2��2mx+m2+m�Ķ���ΪA��
��1����m=1ʱ��ֱ��д�������ߵĶԳ��
��2������A�ڵ�һ���ޣ���OA=![]() ���������ߵĽ���ʽ��
���������ߵĽ���ʽ��
��3����֪��B��m��![]() ��m+1����C��2��2���������������߶�BC�й����㣬��Ϻ���ͼ��ֱ��д��m��ȡֵ��Χ��
��m+1����C��2��2���������������߶�BC�й����㣬��Ϻ���ͼ��ֱ��д��m��ȡֵ��Χ��
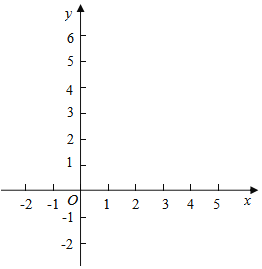
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
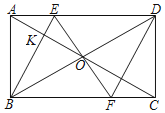
����Ŀ����ͼ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O������O��BD�Ĵ������AD��BC�ֱ��ڵ�E��F������BE��AC�ڵ�K������DF��
��1����֤���ı���EBFD�����Σ�
��2����BK=3EK��AE=4�����ı���EBFD���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ٹ����¿�������״�����Ķ���������õ�����Ч���ƣ����ڸ�����ҵ��2��9�պ���븴��״̬��Ϊ���˽�ȫ����ҵ����ĸ�����������Dz����˽�ֹ��2020��3��1��ȫ������ʡ�ݵĸ����ʣ��������ݽ��������������ͷ��������������һЩ��Ϣ��

a����ֹ3��1��20ʱ��ȫ������11��ʡ�ݹ�ҵ��ҵ��������90%���ϣ���Ҫλ�ڶ����غ�������λ��ǰ���ķֱ��ǹ��ݣ�100%�����㽭��99.8%�������գ�99%����
b����ʡ�ݸ��������ݵ�Ƶ���ֲ�ֱ��ͼ��ͼ1�����ݷֳ�6�飬�ֱ���40��x��50��
50��x��60��60��x��70��70��x��80��80��x��90��90��x��100����
c����ͼ2����b�Ļ����ϣ���������ͳ��ͼ��
d����ֹ��2020��3��1�ո�ʡ�ݵĸ�������80��x��90��һ��������ǣ�
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e����ֹ��2020��3��1�ո�ʡ�ݵĸ����ʵ�ƽ��������λ�����������£�
���� | ƽ���� | ��λ�� | ���� |
��ֹ��2020��3��1�� | 80.79 | m | 50��90 |
�����������⣺
��1���������⣬��ȫƵ���ֲ�ֱ��ͼ��
��2������ͳ��ͼ��50��x��60�����Բ�ĽǶ������� ���ȣ���ȷ��0.1����
��3����λ��m��ֵ���� ����
��4����������ͳ��ͼ������������ҵ��ֹ3��1�յĸ����ʷֲ�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com