
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.
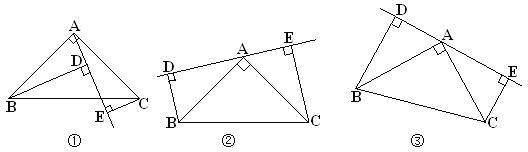
(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
【答案】(1)、证明过程见解析;(2)、BD=DE–CE;证明过程见解析;(3)、BD=DE–CE;(4)、当B,C在AE的同侧时,BD=DE–CE;当B,C在AE的异侧时,BD=DE+CE.
【解析】
试题分析:(1)、根据垂直得出∠ADB=∠CEA=90°,结合∠BAC=90°得出∠ABD=∠CAE,从而证明出△ABD和△ACE全等,根据全等得出BD=AE,AD=EC,然后得出答案;(2)、根据第一题同样的方法得出△ABD和△ACE全等,根据全等得出BD=AE,AD=EC,然后得出结论;(3)、根据同样的方法得出结论;(4)、根据前面的结论得出答案.
试题解析:(1)∵BD⊥AE,CE⊥AE ∴∠ADB=∠CEA=90° ∴∠ABD+∠BAD=90° 又∵∠BAC=90°
∴∠EAC+∠BAD=90° ∴∠ABD=∠CAE
在△ABD与△ACE ∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE+CE
∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE+CE
(2)、∵BD⊥AE,CE⊥AE ∴∠ADB=∠CEA=90° ∴∠ABD+∠BAD=90°
又∵∠BAC=90°∴∠EAC+∠BAD=90° ∴∠ABD=∠CAE
在△ABD与△ACE ∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE–CE
∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE–CE
(3)、BD=DE–CE
(4)、归纳:由(1)(2)(3)可知:当B,C在AE的同侧时,BD = DE –CE;当B,C在AE的异侧时,∴BD=DE+CE


科目:初中数学 来源: 题型:
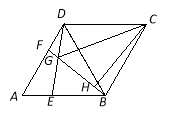
【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=![]() ,BG=
,BG=![]() ,且
,且![]() 、
、![]() 满足下列关系:
满足下列关系:![]() ,
,![]() ,则GH= .
,则GH= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
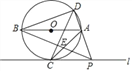
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABC中,∠C=90,BD是
ABC中,∠C=90,BD是![]() ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,

(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
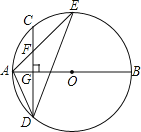
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求证:tan∠E=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
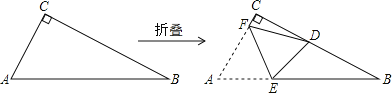
【题目】如图,△ABC中,∠ACB=90°,AC<BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
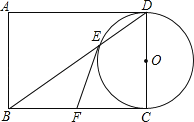
【题目】如图,以矩形ABCD的边CD为直径作⊙O,交矩形的对角线BD于点E,点F是BC的中点,连接EF.
(1)试判断EF与⊙O的位置关系,并说明理由.
(2)若DC=2,EF=![]() ,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对学生就“食品安全知识”进行了抽样调查(每人选填一类),绘制了如图所示的两幅统计图(不完整)。请根据图中信息,解答下列问题:
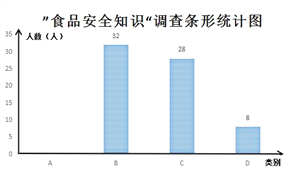
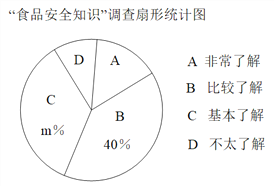
(1)根据图中数据,求出扇形统计图中![]() 的值,并补全条形统计图。
的值,并补全条形统计图。
(2)该校共有学生900人,估计该校学生对“食品安全知识”非常了解的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com