
 如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中全等三角形的对数为( )
如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中全等三角形的对数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由OP平分∠MON,PE⊥OM于E,PF⊥ON于F,得到PE=PF,∠1=∠2,证得△AOP≌△BOP,再根据△AOP≌△BOP,得出AP=BP,于是证得△AOP≌△BOP和Rt△AOP≌Rt△BOP.
解答 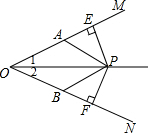 解:∵OP平分∠MON,PE⊥OM于E,PF⊥ON于F,
解:∵OP平分∠MON,PE⊥OM于E,PF⊥ON于F,
∴PE=PF,∠1=∠2,
在△AOP与△BOP中,
$\left\{\begin{array}{l}{OA=OB}\\{∠1=∠2}\\{OP=OP}\end{array}\right.$,
∴△AOP≌△BOP(SAS),
∴AP=BP,
在△EOP与△FOP中,
$\left\{\begin{array}{l}{∠1=∠2}\\{∠OEO=∠OFP=90°}\\{OP=OP}\end{array}\right.$,
∴△EOP≌△FOP(AAS),
在Rt△AOP与Rt△BOP中,
$\left\{\begin{array}{l}{PA=PB}\\{PE=PF}\end{array}\right.$,
∴Rt△AOP≌Rt△BOP(HL_,
∴图中有3对全等三角形.
故选:C.
点评 本题考查了角平分线的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,DE=4cm,则BC的长为( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,DE=4cm,则BC的长为( )| A. | 8cm | B. | 12cm | C. | 11cm | D. | 10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在等腰△ABC中,∠BAC=120°,若EM和FN分别垂直平分AB和AC,垂足分别为E、F、M、N都在BC边上,且EM=FN=4,则BC的长度为( )
如图所示,在等腰△ABC中,∠BAC=120°,若EM和FN分别垂直平分AB和AC,垂足分别为E、F、M、N都在BC边上,且EM=FN=4,则BC的长度为( )| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
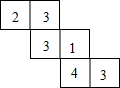 一个几何体由若干个大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示.其中小正方形中的数字表示在该位置小立方块的个数,请你画出从正面和从左面看到的这个几何体的形状图.
一个几何体由若干个大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示.其中小正方形中的数字表示在该位置小立方块的个数,请你画出从正面和从左面看到的这个几何体的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com