
【题目】已知,如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上的一点且GH⊥EG.求证:PF∥GH.

【答案】(1)见解析;(2)见解析.
【解析】
(1)根据对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补,所以易证AB∥CD;
(2)根据(1)中平行线的性质推知°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件GH⊥EG,易证PF∥GH.
:(1)AB∥CD;
理由:如图1,∵∠1与∠2互补,
∴∠1+∠2=180°.
又∵∠1=∠AEF,∠2=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)如图2,由(1)知,AB∥CD,
∴∠BEF+∠EFD=180°.
又∵∠BEF与∠EFD的角平分线交于点P,
∴∠FEP+∠EFP=![]() (∠BEF+∠EFD)=90°,
(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF.
∵GH⊥EG,
∴PF∥GH.


科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与 图书馆的路程是 ![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线 ![]() 和线段
和线段 ![]() 分别表示两人离学校的路程
分别表示两人离学校的路程 ![]() (千米)与所经过的 时间
(千米)与所经过的 时间 ![]() (分钟)之间的函数关系,请根据图像回答下列问题:
(分钟)之间的函数关系,请根据图像回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟;小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程 ![]() (千米)与所经过的时间
(千米)与所经过的时间 ![]() (分钟)之间的函数表达式;
(分钟)之间的函数表达式;
(3)若设两人在路上相距不超过 ![]() 千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2. 
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离. (结果精确到 1cm.参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75≈3.7321
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
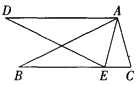
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时,某校根据实际,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目,为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.

(1)请计算最喜欢B项目的人数所占的百分比.
(2)请计算D项所在扇形图中的圆心角的度数.
(3)请把统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF、EC,且CF=EF,下列结论正确的个数是( )
①CF平分∠BCD;②∠EFC=2∠CFD;③∠ECD=90°;④CE⊥AB.
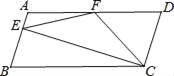
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在(1)![]() (2)
(2) ![]() (3)
(3) ![]() (4)
(4) ![]() 中,________是方程7x-3y=2的解;________是方程2x+y=8的解;________是方程组
中,________是方程7x-3y=2的解;________是方程2x+y=8的解;________是方程组![]() 的解.(填序号)
的解.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
A.600m
B.500m
C.400m
D.300m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com