
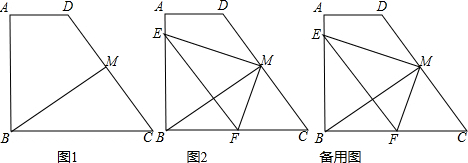
分析 (1)根据M在边CD上,$\frac{DM}{MC}$=$\frac{2}{3}$,得出DM=$\frac{2}{5}$CD,MC=$\frac{3}{5}$CD,再将CD=10代入计算即可求出DM,CM的长度;
(2)如图1,连结BD.根据等腰三角形的性质、平行线的性质得出∠ADB=∠CBD=∠CDB.再利用SAS证明△ADB≌△MDB,根据全等三角形对应角相等得出
∠A=∠BMD=90°,即BM⊥DC;
(3)如图2,根据同角的余角相等得出∠1=∠2,∠ABM=∠C,那么△CMF∽△BME,根据相似三角形对应边成比例得出$\frac{CF}{BE}$=$\frac{CM}{BM}$.设BF=x,列出关于x的方程,得出BE=$\frac{4}{3}$(10-x),根据S△EBF=$\frac{1}{2}$BF•BE,得出S关于x的二次函数解析式,然后根据二次函数的性质即可求解.
解答 (1)解:∵CD=10,M在边CD上,$\frac{DM}{MC}$=$\frac{2}{3}$,
∴DM=$\frac{2}{5}$CD=$\frac{2}{5}$×10=4,MC=$\frac{3}{5}$CD=$\frac{3}{5}$×10=6.
故答案为4,6;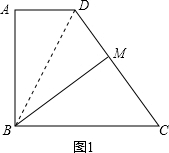 (2)证明:如图1,连结BD.
(2)证明:如图1,连结BD.
∵BC=CD=10,
∴∠CDB=∠CBD,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠ADB=∠CDB.
在△ADB与△MDB中,
$\left\{\begin{array}{l}{AD=MD=4}\\{∠ADB=∠MDB}\\{BD=BD}\end{array}\right.$,
∴△ADB≌△MDB(SAS),
∴∠A=∠BMD=90°,
∴BM⊥DC;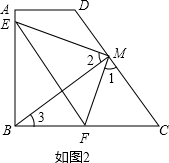 (3)解:如图2,由(2)得∠BMC=90°,
(3)解:如图2,由(2)得∠BMC=90°,
∴∠1+∠BMF=90°,∠C+∠3=90°.
∵∠EMF=90°,
∴∠2+∠BMF=90°,
∴∠1=∠2.
又∵∠ABC=∠A=90°,
∴∠3+∠ABM=90°,
∴∠ABM=∠C.
在△CMF与△BME中,
$\left\{\begin{array}{l}{∠C=∠EBM}\\{∠1=∠2}\end{array}\right.$,
∴△CMF∽△BME,
∴$\frac{CF}{BE}$=$\frac{CM}{BM}$.
在Rt△BCM中,BM=$\sqrt{B{C}^{2}-C{M}^{2}}$=8.
设BF=x,则CF=10-x,
∴$\frac{10-x}{BE}$=$\frac{6}{8}$,
∴BE=$\frac{4}{3}$(10-x),
∴S△EBF=$\frac{1}{2}$BF•BE
=$\frac{1}{2}$x•$\frac{4}{3}$(10-x)
=$\frac{2}{3}$(-x2+10x)
=-$\frac{2}{3}$(x-5)2+$\frac{50}{3}$,
∵-$\frac{2}{3}$<0,
∴当x=5时,S△EBF最大,最大值为$\frac{50}{3}$.
故当BF=5时,△EBF的面积最大,最大值为$\frac{50}{3}$.
点评 本题是四边形综合题,考查了等腰三角形的性质,平行线的性质,全等三角形、相似三角形的判定与性质,勾股定理,三角形的面积,二次函数的性质等知识,综合性较强,难度适中.利用数形结合以及方程思想是解题的关键.


科目:初中数学 来源: 题型:填空题
| 节电量/度 | 2 | 3 | 4 | 5 | 6 |
| 家庭数/个 | 5 | 12 | 12 | 8 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
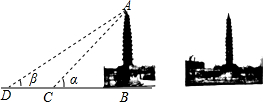 聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早起,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据:$\sqrt{10}$≈3.162)( )
聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早起,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据:$\sqrt{10}$≈3.162)( )| A. | 15.81米 | B. | 16.81米 | C. | 30.62米 | D. | 31.62米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,0) | C. | (-$\frac{1}{3}$,$\frac{2}{3}$) | D. | ($\frac{1}{3}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 圆的面积S与它的半径r | |
| B. | 正方形的周长C与它的边长a | |
| C. | 三角形面积一定时,它的底边a和底边上的高h | |
| D. | 路程不变时,匀速通过全程所需要的时间t与运动的速度v |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com