
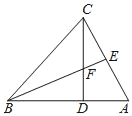
【题目】如图,在△CBD中,CD=BD,CD⊥BD,BE平分∠CBA交CD于点F,CE⊥BE垂足是E,CE与BD交于点A.求证:
(1)BF=AC;
(2)BE是AC的中垂线;
(3)若AD=2,求AB的长.
【答案】(1)见解析;(2)见解析;(3)4+2![]() .
.
【解析】
(1)由 CD⊥AB,BE⊥AC,可得BDF=∠ADC=∠AEB=90°,DBF=∠DCA,继而证明出△BDF≌△CDA可得结论;
(2) BE平分∠ABC,可证∠A=∠BCA,BC=BA ,CE=EA可得结论;
(3) 由(1)BDF≌△CDA,可得各边的长,可求出AB的长.
(1)证明:∵CD⊥AB,BE⊥AC,
∴∠BDF=∠ADC=∠AEB=90°,
∵∠DBF+∠A=90°,∠DCA+∠A=90°,
∴∠DBF=∠DCA,
∵BD=CD,
∴△BDF≌△CDA(SAS),
∴BF=AC.
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠BEA=∠BEC=90°,
∴∠A+∠ABE=90°,∠BCA+∠CBE=90°,
∴∠A=∠BCA,
∴BC=BA,
∵BE⊥AC,
∴CE=EA,
∴BE是AC的中垂线.
(3)解:连接AF.

∵△BDF≌△CDA,
∴AD=DF=2,AF=2![]() ,
,
∵BE垂直平分AC,
∴CF=AF=2![]() ,
,
∴BD=CD=2+2![]() ,
,
∴AB=BD+AD=4+2![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生去福利院献爱心,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)向甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2400元,那么最多可购买多少个甲礼品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索. 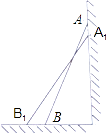
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
(1)请你将小明对“思考题”的解答补充完整: 解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1= ![]() ﹣0.4=2
﹣0.4=2
而A1B1=2.5,在Rt△A1B1C中,由 ![]() 得方程 ,
得方程 ,
解方程得x1= , x2= ,
∴点B将向外移动米.
(2)解完“思考题”后,小聪提出了如下两个问题: 【问题一】在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
【问题二】在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在线段CD上,AE,BE分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-4|=0.
(1)求AD和BC的长;
(2)你认为AD和BC有怎样的位置关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
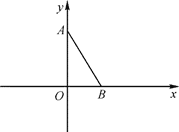
【题目】如图,平面直角坐标系 xOy 中,已知点 A(0,3),点 B(![]() ,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰的等腰三角形时,称点 C 是线段 AB 的“等长点”
,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰的等腰三角形时,称点 C 是线段 AB 的“等长点”
(1)在点 C1 (-2, ![]() ),点 C2 (0,-2),点 C3 (
),点 C2 (0,-2),点 C3 (![]() ,
, ![]() )中,线段 AB 的“等长点”是点______________;
)中,线段 AB 的“等长点”是点______________;
(2)若点 D( m , n )是线段 AB 的“等长点”,且∠DAB=60,求 m 和 n 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )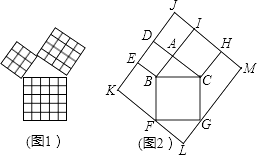
A.90
B.100
C.110
D.121
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=![]() ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com