
 如图,AB=AE,∠1=∠2,∠C=∠D,判断线段BC与线段DE是否相等,并说明理由.
如图,AB=AE,∠1=∠2,∠C=∠D,判断线段BC与线段DE是否相等,并说明理由. 分析 先利用∠1=∠2得到∠BAC=∠DAE,然后根据“AAS”证明△ACB≌△ADE,则根据全等三角形的性质得DE=BC.
解答 解:BC=DE,
理由:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠CAE,
即∠BAC=∠EAD,
在△ABC与△AED中,$\left\{\begin{array}{l}{∠BAC=∠EAD}\\{∠C=∠D}\\{AB=AE}\end{array}\right.$,
∴△ABC≌△AED,
∴BC=DE.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:判断题
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
⑴请画出平移后的△A′B′C′.
(2)△A′B′C′的面积为_________.
(3)若连接AA′,CC′,则这两条线段之间的关系是_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )
如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
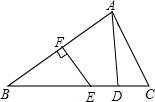 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC.
如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图△ABC,△DMN中∠A=∠MDN=90°,AB=AC=4,D为BC边中点,绕D点转动△DMN.使得DM与线段AB交于E点(不与A、B重合),DN边与线段AC交于F点
如图△ABC,△DMN中∠A=∠MDN=90°,AB=AC=4,D为BC边中点,绕D点转动△DMN.使得DM与线段AB交于E点(不与A、B重合),DN边与线段AC交于F点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x2+2 | B. | y=2(x+2)2 | C. | y=2x2-2 | D. | y=2(x-2)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com