
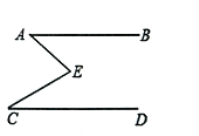
【题目】如图![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() ,
,![]() 之间的一点,连接
之间的一点,连接![]() 、
、![]() .
.
(1)问题发现:
①若![]() ,
,![]() ,则
,则![]() .
.
②猜想图![]() 中
中![]() 、
、![]() 、
、![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
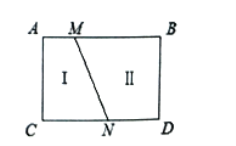
(2)拓展应用:
如图![]() ,
,![]() ,线段
,线段![]() 把
把![]() 这个封闭区域分为
这个封闭区域分为![]() 、
、![]() 两部分(不含边界),点
两部分(不含边界),点![]() 是位于这两个区域内的任意一点(不在边界上),请直接写出
是位于这两个区域内的任意一点(不在边界上),请直接写出![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.
【答案】(1)①![]() ,②
,②![]() ,见解析;(2)当点
,见解析;(2)当点![]() 位于区域
位于区域![]() 时,
时, ![]() ,当点
,当点![]() 位于区域
位于区域![]() 时,
时, ![]() .
.
【解析】
(1)①过点E作EF∥AB,再由平行线的性质即可得出结论;②、根据①的过程可得出结论;
(2)根据题意画出图形,再根据平行线的性质即可得出∠EMB、∠END、∠MEN的关系.
解:(1)
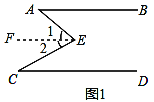
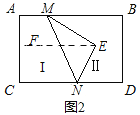
①如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=45°,∠C=30°,
∴∠1=∠A=45°,∠2=∠C=30°,
∴∠AEC=∠1+∠2=75°;
②猜想: ![]() .
.
理由:如图![]() ,过点
,过点![]() 作
作![]() ,
,
∵![]()
∴![]() (平行于同一条直线的两直线平行),
(平行于同一条直线的两直线平行),
∴![]() ,
,![]() (两直线平行,内错角相等),
(两直线平行,内错角相等),
∴![]() (等量代换);
(等量代换);
(2)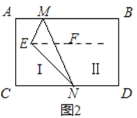
当点![]() 位于区域
位于区域![]() 时,
时, ![]() ,
,
理由:过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BME+∠MEF=180°,∠DNE+∠NEF=180°,
∴∠EMB+∠END+∠MEN=360°;
当点![]() 位于区域
位于区域![]() 时,
时, ![]() .
.
理由:过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BMN=∠FEM,∠DNE=∠FEN,
∴∠EMB+∠END=∠MEF+∠NEF=∠MEN.
故答案为:(1)①![]() ,②
,②![]() ,见解析;(2)当点
,见解析;(2)当点![]() 位于区域
位于区域![]() 时,
时, ![]() ,当点
,当点![]() 位于区域
位于区域![]() 时,
时, ![]() .
.


 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(2k+3)x+k2=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若两不相等的实数根满足![]() -
-![]() -
-![]() =-9,求实数k的值.
=-9,求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点D,下列结论:①△BCD是等腰三角形;②BD是∠ABC的平分线;③DC+BC=AB;④△AMD≌△BCD,正确的是 ( )

A.①②B.②③C.①②③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
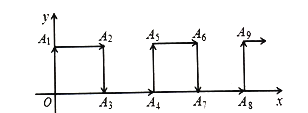
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点
出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点![]() ,
,![]() ,
,![]() ,
,![]() ,...那么点
,...那么点![]() 的坐标为( ).
的坐标为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
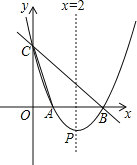
【题目】如图,直线y=﹣x+3与x轴,y轴分别相交于点B,C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)求该抛物线的函数表达式;
(2)请问在抛物线上是否存在点Q,使得以点B,C,Q为顶点的三角形为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由;
(3)过S(0,4)的动直线l交抛物线于M,N两点,试问抛物线上是否存在定点T,使得不过定点T的任意直线l都有∠MTN=90°?若存在,请求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧![]() 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com