
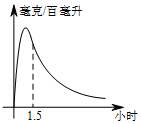
 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)分析 (1)利用y=-200x2+400x=-200(x-1)2+200确定最大值;
(2)①先求出反比例函数解析式,再分别求得y≥80时x的范围,即可知醉酒持续的时间;②计算出反比例函数中y<20时x的范围,就可得酒精含量低于20所需时间.
解答 解:(1)y=-200x2+400x=-200(x-1)2+200,
∴x=1时血液中的酒精含量达到最大值,最大值为200(毫克/百毫升);
(2)①当x=1.5时,y=-200x2+400x=-200×2.25+400×1.5=150,
∴k=1.5×150=225,
即x>1.5时,y=$\frac{225}{x}$;
当0<x≤1.5时,由-200(x-1)2+200≥80,
解得:5-$\sqrt{15}$≤x≤5+$\sqrt{15}$,
当x>1.5时,由$\frac{225}{x}$≥80得x≤$\frac{45}{16}$,
则当5-$\sqrt{15}$≤x≤$\frac{45}{16}$时,其酒精含量属于“醉酒驾车”范围;
$\frac{45}{16}$-5+$\sqrt{15}$≈1.8,
答:有1.8小时其酒精含量属于“醉酒驾车”范围;
②由$\frac{225}{x}$<20可得x>11.25,
即从饮酒后11.25小时才能驾车去上班,
则第二天早上7:15才能驾车去上班.
点评 此题主要考查了二次函数和反比例函数综合应用,根据图象得出正确信息是解题关键,能够从实际问题中抽象出二次函数模型是解答的重点.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
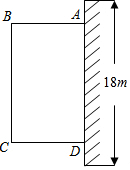 为了改善小区环境,某小区决定要在一块一边靠墙(墙长18m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图),设绿化带BC边长为xm,绿化带的面积为ym2.
为了改善小区环境,某小区决定要在一块一边靠墙(墙长18m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图),设绿化带BC边长为xm,绿化带的面积为ym2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
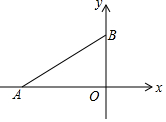 如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).
如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com