
【题目】如图,已知点D为等腰直角△ABC内一点,∠ACB=90°,AD=BD,∠BAD=30°,E为AD延长线上的一点,且CE=CA,若点M在DE上,且DC=DM.则下列结论中:①∠ADB=120°;②△ADC≌△BDC;③线段DC所在的直线垂直平分线AB;④ME=BD;正确的有( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
由等腰三角形的性质可判断①,由“SSS”可证△ADC≌△BDC,可判断②,由全等三角形的性质和等腰三角形的性质可判断③,由“AAS”可证△ACD≌△ECM,可判断④.
解:∵AD=BD,∠BAD=30°,
∴∠BAD=∠ABD=30°,
∴∠ADB=120°,
故①正确;
∵AC=BC,AD=BD,CD=CD,
∴△ADC≌△BDC(SSS),
故②正确;
∵△ADC≌△BDC
∴∠ACD=∠BCD,且AC=BC
∴线段DC所在的直线垂直平分线AB,
故③正确;
∵△ABC是等腰直角三角形,
∴∠CAB=∠CBA,
∴∠CAD=∠CBD=15°,
∵CA=CE,
∴∠E=∠CAD=15°,
∵∠EDC=∠DAC+∠DCA=60°,且CD=CM,
∴∠CDE=∠CMD=60°,
∴∠ADC=∠CME=120°,且∠E=∠CAD,AC=CE,
∴△ACD≌△ECM(AAS),
∴AD=ME=BD,
故④正确,
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
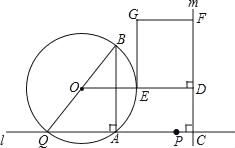
【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=![]() CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某种新能源汽车的性能,对这种汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)这次被抽检的新能源汽车共有 辆;
(2)将图1补充完整;在图2中,C等级所占的圆心角是 度;
(3)估计这种新能源汽车一次充电后行驶的平均里程数为多少千米?(精确到千米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为K90的化学赛道,其中助滑坡AB长90米,坡角a=40°,一个曲面平台BCD连接了助滑坡AB与着陆坡,某运动员在C点飞向空中,几秒之后落在着陆坡上的E处,已知着陆坡DE的坡度i=1: ![]() ,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)
,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)

A. 101.4 B. 101.3 C. 100.4 D. 100.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某网络公司员工月收人情况表.
月收入(元) |
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
(1)求此公司员工月收人的中位数;
(2)小张求出这个公司员工月收人平均数为![]() 元,若用所求平均数反映公司全体员工月收人水平,合适吗?若不合适,用什么数据更好?
元,若用所求平均数反映公司全体员工月收人水平,合适吗?若不合适,用什么数据更好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=3cm,∠B=30°,点D在BC边上由C向B匀速运动(D不与B、C重合),匀速运动速度为1cm/s,连接AD,作∠ADE=30°,DE交线段AC于点E.
(1)在此运动过程中,∠BDA逐渐变 (填“大”或“小”);D点运动到图1位置时,∠BDA=75°,则∠BAD= .
(2)点D运动3s后到达图2位置,则CD= .此时△ABD和△DCE是否全等,请说明理由;
(3)在点D运动过程中,△ADE的形状也在变化,判断当△ADE是等腰三角形时,∠BDA等于多少度(请直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:
(1)直接写出点A的坐标,点A关于x轴的对称点B的坐标,点B关于y轴的对称点C的坐标.
(2)画出将线段BC向右平移2个单位,再向上平移4个单位后的线段B′C′,并直接写出B′的坐标.
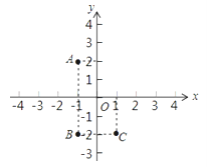
查看答案和解析>>
科目:初中数学 来源: 题型:
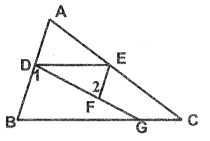
【题目】已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 ∥ ( )
所以∠B+∠BDE=180°( )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180°( )
所以 ∥ ( )
所以∠1=∠2( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com