
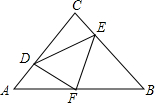
 如图,在等腰直角△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF,在此运动变化的过程中,下列结论:
如图,在等腰直角△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF,在此运动变化的过程中,下列结论:分析 连结CF,如图,根据等腰直角△ABC的性质得CF=AF=BF,CF⊥AB,∠1=45°,则可根据“SAS”判断△ADF≌△CEF,得到DF=EF,∠3=∠2,由∠3+∠CFD=90°可得∠3+∠2=90°,即∠DFE=90°,所以△DEF为等腰直角三角形,于是可对①进行判断;由于当FD⊥AC时,FE⊥BC,则AD=CE=$\frac{1}{2}$AC,此时四边形CDFE为正方形,于是可对③进行判断;利用S△ADF=S△CEF可得四边形CDFE的面积=S△ACF=$\frac{1}{2}$S△ABC=16,于是可对②进行判断;由于S△CDE=S四边形CDFE-S△DEF=16-S△DEF,FD的长度的最小值为4,则S△DEF的最小值值为8,所以△CDE面积的最大值为8,则可对④进行判断,问题得解.
解答 解:连结CF,如图,
∵△ABC为直角三角形,
∴∠A=45°,
∵F是等腰直角△ABC斜边上的中点,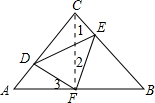
∴CF=AF=BF,CF⊥AB,∠1=45°,
在△ADF和△CEF中,
$\left\{\begin{array}{l}{AD=CE}\\{∠A=∠1}\\{AF=CF}\end{array}\right.$,
∴△ADF≌△CEF(SAS),
∴DF=EF,∠3=∠2,
∵∠3+∠CFD=90°,
∴∠3+∠2=90°,即∠DFE=90°,
∴△DEF为等腰直角三角形,所以①正确;
∵△ADF≌△CEF,
∴S△ADF=S△CEF,
∴四边形CDFE的面积=S△ACF=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×8×8=16,所以②正确;
当FD⊥AC时,FE⊥BC,则AD=CE=$\frac{1}{2}$AC,此时四边形CDFE为正方形,所以③正确;
∵S△CDE=S四边形CDFE-S△DEF=16-S△DEF,
而当FD⊥AC时,FD的长度最小,此时FD=$\frac{1}{2}$AC=4,
∴S△DEF的最小值为$\frac{1}{2}$×4×4=8,
∴△CDE面积的最大值为16-8=8,所以④正确.
故答案为③
点评 本题考查的是和四边形有关的综合性题目,用到的知识点有:正方形的判定、等腰直角三角形的性质、全等三角形的判定和性质,掌握正方形的判定定理、全等三角形的判定定理和性质定理、熟记各种特殊几何图形的性质是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6ab=2a•3b | B. | x2-4+3x=(x+2)( x-2)+3x | ||
| C. | x2-9=( x+3)( x-3) | D. | (x+2)( x-2)=x2-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com