
 已知:如图,半径都是5cm的两等圆⊙O1和⊙O2相交于点A,B,过A作⊙O1的直径AC与⊙O2交于点D,且AD:DC=3:2,E为DC的中点.
已知:如图,半径都是5cm的两等圆⊙O1和⊙O2相交于点A,B,过A作⊙O1的直径AC与⊙O2交于点D,且AD:DC=3:2,E为DC的中点.分析 (1)根据已知条件得到AD=6,DC=4,由E为DC的中点.得到DE=EC=2,AD=6作O2F⊥AB于F点,则AF=FD=3,FE=FD+DE=3+2=5,推出四边形AO1O2B是菱形.根据菱形的性质得到O2B∥AC∥FE,推出O2BEF是矩形.于是得到AC⊥BE;
(2)根据勾股定理即可得到结论.
解答 解:(1)∵两等圆的半径为5,
∴AC=10,
∵AD:DC=3:2,
∴令AD=3a,DC=2a,
∵AD+DC=AC=10,
∴a=2,
∴AD=6,DC=4,
∵E为DC的中点.
∴DE=EC=2,AD=6
作O2F⊥AB于F点,则AF=FD=3,FE=FD+DE=3+2=5,
∵AO1=AO2=BO1=BO2=5.
∴四边形AO1O2B是菱形.
∴O2B∥AC∥FE,
又知FE=5=O2B,
∴O2BEF是平行四边形,
而O2F⊥AB于F点,∴O2BEF是矩形.
∴AC⊥BE;
(2)∵O1B=5,AE=AD+DE=8,
∴O1E=AE-5=3,
∴BE=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=4$\sqrt{5}$.
点评 本题考查了相交两圆的性质,菱形的判定和性质,就行的判定和性质,勾股定理,垂径定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,对于点P和⊙O给出如下定义:若⊙O上存在两个点A、B,使得∠APB=60°,则称P为⊙O的关联点.
在平面直角坐标系xOy中,对于点P和⊙O给出如下定义:若⊙O上存在两个点A、B,使得∠APB=60°,则称P为⊙O的关联点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
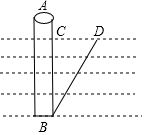 桥梁工程师想探知50m高的一根桥桩是否与地面垂直,他用铅锤系着一根与桥桩等长的绳子沉到桥桩底部,这时发现水面向上露出10m(AC),再斜拉绳子的端点A到水面的D处,测得CD=30m,根据这位工程师测得的数据,判断桥桩与地面是否垂直.
桥梁工程师想探知50m高的一根桥桩是否与地面垂直,他用铅锤系着一根与桥桩等长的绳子沉到桥桩底部,这时发现水面向上露出10m(AC),再斜拉绳子的端点A到水面的D处,测得CD=30m,根据这位工程师测得的数据,判断桥桩与地面是否垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com