
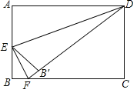
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接ED,则DE的长度是_____,B′D的最小值是_____.
科目:初中数学 来源: 题型:
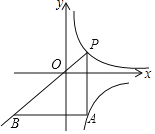
【题目】如图,在平面直角坐标系中,点P在函数y=![]() (x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣
(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣![]() (x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
A.逐渐变大B.逐渐变小C.等于定值16D.等于定值24
查看答案和解析>>
科目:初中数学 来源: 题型:
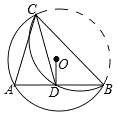
【题目】如图,在⊙O中,点C在优弧![]() 上,将
上,将![]() 沿BC折叠后刚好经过AB的中点D,连接AC,CD.则下列结论中错误的是( )
沿BC折叠后刚好经过AB的中点D,连接AC,CD.则下列结论中错误的是( )
①AC=CD;②AD=BD;③![]() +
+![]() =
=![]() ;④CD平分∠ACB
;④CD平分∠ACB
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,弦AB=![]() ,BC=
,BC=![]() ,AB,BC在圆心O的两侧,弧AC上有一动点D,AE⊥BD于点E,当点D从点C运动到点A时,则点E所经过的路径长为__________.
,AB,BC在圆心O的两侧,弧AC上有一动点D,AE⊥BD于点E,当点D从点C运动到点A时,则点E所经过的路径长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
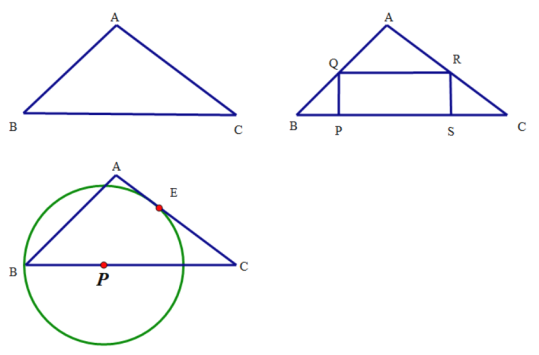
【题目】如图1,在△ABC中,∠ABC=45°,BC=7cm,AB=![]() cm。点P从点B出发沿BC方向向点C运动,当点P到点C时,停止运动
cm。点P从点B出发沿BC方向向点C运动,当点P到点C时,停止运动
(1)如图2,过点P作PQ⊥BC,PQ交AB于点Q,以PQ为一边向右侧作矩形PQRS,若点R恰好在边AC上,且满足QR=2PQ.求BP得值.
(2)以点P为圆心,BP为半径作圆.
①如图3,当⊙P与边AC相切于点E时,求BP的值;
②随着BP的变化,⊙P与△ABC三边的公共点的个数也在变化,请直接写出公共点个数与对应的BP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形MNPQ中,动点R从点N出发,沿着N-P-Q-M方向移动至M停止,设R移动路程为x,MNR面积为y,那么y与x的关系如图②,下列说法不正确的是( )
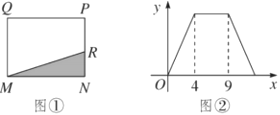
A.当x=2时,y=5B.矩形MNPQ周长是18
C.当x=6时,y=10D.当y=8时,x=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①抛物线y=ax2+bx+3(a≠0)与x轴,y轴分别交于点A(﹣1,0),B(3,0),点C三点.

(1)试求抛物线的解析式;
(2)点D(2,m)在第一象限的抛物线上,连接BC,BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)点N在抛物线的对称轴上,点M在抛物线上,当以M、N、B、C为顶点的四边形是平行四边形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 的顶点为A.
的顶点为A.
(1)求点A的坐标;

(2)将线段![]() 沿
沿![]() 轴向右平移2个单位得到线段
轴向右平移2个单位得到线段![]() .
.
①直接写出点![]() 和
和![]() 的坐标;
的坐标;
②若抛物线![]() 与四边形
与四边形![]() 有且只有两个公共点,结合函数的图象,求
有且只有两个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”成为我市推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
分组前学生学习兴趣 分组后学生学习兴趣
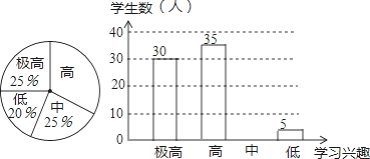
请结合图中信息解答下列问题:
(1)求出分组前学生学习兴趣为“高”的所占的百分比为 ;
(2)补全分组后学生学习兴趣的统计图;
(3)通过“分组合作学习”前后对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com