
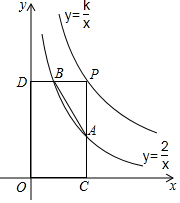
 两个反比例函数y=$\frac{2}{x}$和y=$\frac{k}{x}$(k>2)在第一象限的图象如图所示,第一象限中的点P在y=$\frac{k}{x}$的图象上运动,PC⊥x轴于C,PD⊥y轴于D,PC、PD分别交y=$\frac{2}{x}$的图象于点A,B.
两个反比例函数y=$\frac{2}{x}$和y=$\frac{k}{x}$(k>2)在第一象限的图象如图所示,第一象限中的点P在y=$\frac{k}{x}$的图象上运动,PC⊥x轴于C,PD⊥y轴于D,PC、PD分别交y=$\frac{2}{x}$的图象于点A,B.分析 (1)直接代入点P坐标即可得出结论;
(2)先表示A,B,C,D,P的坐标,进而表示出BP,DP,CD,建立方程求出m,k即可求出AB的长度;
(3)分m=2和m=3两种情况讨论计算:①m=2时,先确定出A,B坐标,进而得出直线AB解析式,进而设出MN的解析式,用平行四边形的性质AB=MN建立方程,求出直线MN解析式,即可得出AC,CM,ON.OM,用锐角三角函数判断出结论,②同①的方法即可.
解答 解:(1)∵P在y=$\frac{k}{x}$的图象上运动,点P的坐标为(3,4),
∴k=3×4=12
(2)∵点A的横坐标为m,
∴A(m,$\frac{2}{m}$),
∴C(m,0),P(m,$\frac{k}{m}$),
∴B($\frac{2m}{k}$,$\frac{k}{m}$),D(0,$\frac{k}{m}$)
∴BP=m-$\frac{2m}{k}$,PD=m,CD=$\sqrt{{m}^{2}+(\frac{k}{m})^{2}}$
∵BP=$\frac{2}{3}$DP,
∴m-$\frac{2m}{k}$=$\frac{2}{3}$m,
∴k=6,
∴CD=$\sqrt{{m}^{2}+(\frac{6}{m}})^{2}$,
∵CD=$\sqrt{13}$,
∴$\sqrt{{m}^{2}+(\frac{6}{m}})^{2}$=$\sqrt{13}$,
∴m=±2或m=±3,
∵第一象限中的点P在y=$\frac{k}{x}$的图象上运动,
∴m=2或m=3,
当m=2时,A(2,1),B($\frac{2}{3}$,3),
∴AB=$\frac{2\sqrt{13}}{3}$,
当m=3时,A(3,$\frac{2}{3}$),B(1,2),
∴AB=$\frac{2\sqrt{13}}{3}$,
即:AB的长度为$\frac{2\sqrt{13}}{3}$;
(3)∠AMC=∠NMO
如图,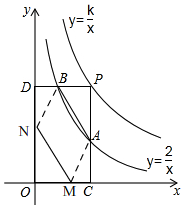
理由:由(2)知,AB=$\frac{2\sqrt{13}}{3}$,
①当m=2时,A(2,1),B($\frac{2}{3}$,3),
∴直线AB解析式为y=-$\frac{3}{2}$x+4,
∵四边形MABN是平行四边形,
∴MN∥AB,MN=AB,
∴设直线MN的解析式为y=-$\frac{3}{2}$x+b,
∴M($\frac{2b}{3}$,0),N(0,b),
∴MN=$\sqrt{(\frac{2b}{3})^{2}+{b}^{2}}$=$\frac{\sqrt{13}}{3}$|b|,
∴$\frac{\sqrt{13}}{3}$|b|=$\frac{2\sqrt{13}}{3}$,
∴b=±2,
∵四边形MABN是平行四边形,
∴b=2,
MN解析式为y=-$\frac{3}{2}$x+2,
∴M($\frac{4}{3}$,0),N(0,2),
∴CM=$\frac{2}{3}$,AC=1,NO=2,OM=$\frac{4}{3}$,
∵C(2,0)
∴OC=2
∵tan∠AMC=$\frac{AC}{MC}$=$\frac{1}{2-\frac{4}{3}}$=$\frac{3}{2}$,tan∠NMO=$\frac{ON}{OM}$=$\frac{2}{\frac{4}{3}}$=$\frac{3}{2}$,
∴tan∠AMC=tan∠NMO,
∵∠AMC,∠NMO是锐角,
∴∠AMC=∠NMO,
②当m=3时,A(3,$\frac{2}{3}$),B(1,2),
∴直线AB解析式为y=-$\frac{2}{3}$x+4,
∵四边形MABN是平行四边形,
∴MN∥AB,MN=AB,
∴设直线MN的解析式为y=-$\frac{2}{3}$x+b',
∴M($\frac{3}{2}$b',0),N(0,b'),
∴MN=$\sqrt{(\frac{3}{2}b')^{2}+b{'}^{2}}$=$\frac{\sqrt{13}}{2}$|b'|,
∴$\frac{\sqrt{13}}{2}$|b'|=$\frac{2\sqrt{13}}{3}$,
∴b'=±$\frac{4}{3}$,
∵四边形MABN是平行四边形,
∴b'=$\frac{4}{3}$
MN解析式为y=-$\frac{2}{3}$x+$\frac{4}{3}$,
∴N(0,$\frac{4}{3}$),M(2,0),
∴AC=$\frac{2}{3}$,CM=1,OM=2,ON=$\frac{4}{3}$,
∵C(3,0),
∴OC=3
∵tan∠AMC=$\frac{AC}{MC}$=$\frac{\frac{2}{3}}{1}$=$\frac{2}{3}$,tan∠NMO=$\frac{ON}{OM}$=$\frac{\frac{4}{3}}{2}$=$\frac{2}{3}$,
∴tan∠AMC=tan∠NMO,
∵∠AMC,∠NMO是锐角,
∴∠AMC=∠NMO.
即:∠AMC=∠NMO.
点评 此题是反比例函数综合题,主要考查了待定系数法,平面坐标系内,两点间的距离公式,平行四边形的性质,锐角三角函数,解本题的关键是用方程的思想解决问题,是一道比较简单的中考常考题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
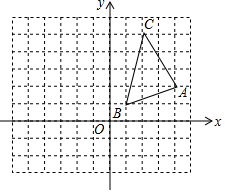 △ABC在平面直角坐标系中的位置如图所示,其中A、B、C三点在格点上.
△ABC在平面直角坐标系中的位置如图所示,其中A、B、C三点在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com