
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¾ŲŠĪOCDEµÄ¶„µćCŗĶE·Ö±šŌŚyÖįµÄÕż°ėÖįŗĶxÖįµÄÕż°ėÖįÉĻ£¬OC=8£¬OE=17£¬Å×ĪļĻßy=![]() x2©3x+mÓėyÖįĻą½»ÓŚµćA£¬Å×ĪļĻߵĶŌ³ĘÖįÓėxÖįĻą½»ÓŚµćB£¬ÓėCD½»ÓŚµćK£®
x2©3x+mÓėyÖįĻą½»ÓŚµćA£¬Å×ĪļĻߵĶŌ³ĘÖįÓėxÖįĻą½»ÓŚµćB£¬ÓėCD½»ÓŚµćK£®
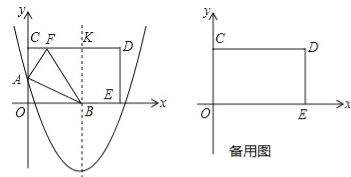
£Ø1£©½«¾ŲŠĪOCDEŃŲABÕŪµž£¬µćOĒ”ŗĆĀäŌŚ±ßCDÉĻµÄµćF“¦£®
¢ŁµćBµÄ×ų±źĪŖ£Ø ”¢ £©£¬BKµÄ³¤ŹĒ £¬CKµÄ³¤ŹĒ £»
¢ŚĒóµćFµÄ×ų±ź£»
¢ŪĒėÖ±½ÓŠ“³öÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©½«¾ŲŠĪOCDEŃŲמ¹żµćEµÄÖ±ĻßÕŪµž£¬µćOĒ”ŗĆĀäŌŚ±ßCDÉĻµÄµćG“¦£¬Į¬½ÓOG£¬ÕŪŗŪÓėOGĻą½»ÓŚµćH£¬µćMŹĒĻ߶ĪEHÉĻµÄŅ»øö¶Æµć£Ø²»ÓėµćHÖŲŗĻ£©£¬Į¬½ÓMG£¬MO£¬¹żµćG×÷GP”ĶOMÓŚµćP£¬½»EHÓŚµćN£¬Į¬½ÓON£¬µćM“ÓµćEæŖŹ¼ŃŲĻ߶ĪEHĻņµćHŌĖ¶Æ£¬ÖĮÓėµćNÖŲŗĻŹ±Ķ£Ö¹£¬”÷MOGŗĶ”÷NOGµÄĆ껿·Ö±š±ķŹ¾ĪŖS1ŗĶS2£¬ŌŚµćMµÄŌĖ¶Æ¹ż³ĢÖŠ£¬S1S2£Ø¼“S1ÓėS2µÄ»ż£©µÄÖµŹĒ·ń·¢Éś±ä»Æ£æČō±ä»Æ£¬ĒėÖ±½ÓŠ“³ö±ä»Æ·¶Ī§£»Čō²»±ä£¬ĒėÖ±½ÓŠ“³öÕāøöÖµ£®
ĪĀÜ°ĢįŹ¾£ŗæ¼ÉśæÉŅŌøł¾ŻĢāŅā£¬ŌŚ±øÓĆĶ¼ÖŠ²¹³äĶ¼ŠĪ£¬ŅŌ±ć×÷“š£®
”¾“š°ø”æ£Ø1£©¢Ł10£¬0£¬8£¬10£»¢Ś£Ø4£¬8£©£»¢Ūy=![]() x2©3x+5.£Ø2£©²»±ä£®S1S2=189£®
x2©3x+5.£Ø2£©²»±ä£®S1S2=189£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©¢Łøł¾ŻĖıߊĪOCKBŹĒ¾ŲŠĪŅŌ¼°¶Ō³ĘÖį¹«Ź½¼“æɽā¾öĪŹĢā£®¢ŚŌŚRT”÷BKFÖŠĄūÓĆ¹“¹É¶ØĄķ¼“æɽā¾öĪŹĢā£®¢ŪÉčOA=AF=x£¬ŌŚRT”÷ACFÖŠ£¬AC=8©x£¬AF=x£¬CF=4£¬ĄūÓĆ¹“¹É¶ØĄķ¼“æɽā¾öĪŹĢā£®
£Ø2£©²»±ä£®S1S2=189£®ÓÉ”÷GHN”×”÷MHG£¬µĆ![]() £¬µĆµ½GH2=HNHM£¬Ēó³öGH2£¬øł¾ŻS1S2=
£¬µĆµ½GH2=HNHM£¬Ēó³öGH2£¬øł¾ŻS1S2=![]() OGHN
OGHN![]() OGHM¼“æɽā¾öĪŹĢā£®
OGHM¼“æɽā¾öĪŹĢā£®
ŹŌĢā½āĪö£ŗ£Ø1£©ČēĶ¼1ÖŠ£¬¢Ł”ßÅ×ĪļĻßy=![]() x2©3x+mµÄ¶Ō³ĘÖįx=©
x2©3x+mµÄ¶Ō³ĘÖįx=©![]() =10£¬
=10£¬
”ąµćB×ų±ź£Ø10£¬0£©£¬
”ßĖıߊĪOBKCŹĒ¾ŲŠĪ£¬
”ąCK=OB=10£¬KB=OC=8£¬
¹Ź“š°ø·Ö±šĪŖ10£¬0£¬8£¬10£®
¢ŚŌŚRT”÷FBKÖŠ£¬”ß”ĻFKB=90”ć£¬BF=OB=10£¬BK=OC=8£¬
”ąFK=![]() =6£¬
=6£¬
”ąCF=CK©FK=4£¬
”ąµćF×ų±ź£Ø4£¬8£©£®
¢ŪÉčOA=AF=x£¬
ŌŚRT”÷ACFÖŠ£¬”ßAC2+CF2=AF2£¬
”ą£Ø8©x£©2+42=x2£¬
”ąx=5£¬
”ąµćA×ų±ź£Ø0£¬5£©£¬“śČėÅ×ĪļĻßy=![]() x2©3x+mµĆm=5£¬
x2©3x+mµĆm=5£¬
”ąÅ×ĪļĻßĪŖy=![]() x2©3x+5£®
x2©3x+5£®
£Ø2£©²»±ä£®S1S2=189£®
ĄķÓÉ£ŗČēĶ¼2ÖŠ£¬ŌŚRT”÷EDGÖŠ£¬”ßGE=EO=17£¬ED=8£¬
”ąDG=![]() =15£¬
=15£¬
”ąCG=CD©DG=2£¬
”ąOG=![]() =2
=2![]() £¬
£¬
”ßCP”ĶOM£¬MH”ĶOG£¬
”ą”ĻNPN=”ĻNHG=90”ć£¬
”ß”ĻHNG+”ĻHGN=90”ć£¬”ĻPNM+”ĻPMN=90”ć£¬”ĻHNG=”ĻPNM£¬
”ą”ĻHGN=”ĻNMP£¬
”ß”ĻNMP=”ĻHMG£¬”ĻGHN=”ĻGHM£¬
”ą”÷GHN”×”÷MHG£¬
”ą![]() £¬
£¬
”ąGH2=HNHM£¬
”ßGH=OH=![]() £¬
£¬
”ąHNHM=17£¬
ӧS1/span>S2=![]() OGHN
OGHN![]() OGHM=£Ø
OGHM=£Ø![]() 2
2![]() £©217=289£®
£©217=289£®




| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
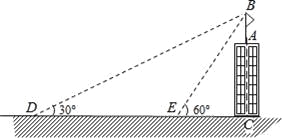
”¾ĢāÄæ”æČēĶ¼£¬Ä³½ØÖžĪļAC¶„²æÓŠŅ»ĘģøĖAB£¬ĒŅµćA£¬B£¬CŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬Š”Ć÷ŌŚµŲĆęD“¦¹Ū²āĘģøĖ¶„¶ĖBµÄŃö½ĒĪŖ30”ć£¬Č»ŗóĖūÕż¶Ō½ØÖžĪļµÄ·½ĻņĒ°½ųĮĖ20Ć×µ½“ļµŲĆęµÄE“¦£¬ÓÖ²āµĆĘģøĖ¶„¶ĖBµÄŃö½ĒĪŖ60”ć£¬ŅŃÖŖ½ØÖžĪļµÄø߶ČAC=12m£¬ĒóĘģøĖABµÄøß¶Č£Ø½į¹ū¾«Č·µ½0.1Ć×£©£®²Īæ¼Źż¾Ż£ŗ![]() ”Ö1.73£¬
”Ö1.73£¬![]() ”Ö1.41£®
”Ö1.41£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
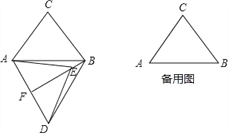
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ,AB=6,AC=BC=5,½«”÷ABCČʵćA°“Ė³Ź±Õė·½ĻņŠż×Ŗ,µĆµ½”÷ADE,Šż×Ŗ½ĒĪŖ¦Į£Ø0”ć£¼¦Į£¼180”ć£©,µćBµÄ¶ŌÓ¦µćĪŖµćD,µćCµÄ¶ŌÓ¦µćĪŖµćE,Į¬½ÓBD£¬BE£®
£Ø1£©ČēĶ¼,µ±¦Į=60”揱,ŃÓ³¤BE½»ADÓŚµćF£®
¢ŁĒóÖ¤£ŗ”÷ABDŹĒµČ±ßČż½ĒŠĪ£»
¢ŚĒóÖ¤£ŗBF”ĶAD£¬AF=DF£»
¢ŪĒėÖ±½ÓŠ“³öBEµÄ³¤£»
£Ø2£©ŌŚŠż×Ŗ¹ż³ĢÖŠ,¹żµćD×÷DG“¹Ö±ÓŚÖ±ĻßAB,“¹×ćĪŖµćG,Į¬½ÓCE,µ±”ĻDAG=”ĻACB,ĒŅĻ߶ĪDGÓėĻ߶ĪAEĪŽ¹«¹²µćŹ±,ĒėÖ±½ÓŠ“³öBE+CEµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
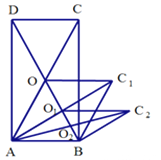
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDµÄĆ껿ĪŖ1cm2£¬¶Ō½ĒĻß½»ÓŚµćO£»ŅŌAB”¢AOĪŖĮŚ±ß×öĘ½ŠŠĖıߊĪAOC1B£¬¶Ō½ĒĻß½»ÓŚµćO1£»ŅŌAB”¢AO1ĪŖĮŚ±ß×öĘ½ŠŠĖıߊĪAO1C2B””£»ŅĄ“ĖĄąĶĘ£¬ŌņĘ½ŠŠĖıߊĪ![]() µÄĆ껿ĪŖ£Ø £©
µÄĆ껿ĪŖ£Ø £©
A. ![]() B.
B. ![]() C.
C. ![]() D£®
D£®![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øöČż½ĒŠĪµÄČżøöÄŚ½ĒµÄ¶ČŹż±ČŹĒ1 ”Ć6 ”Ć5 £¬×ī“óµÄŅ»øöÄŚ½ĒŹĒ__________¶Č£¬°“½Ē·Ö£¬ĖüŹĒŅ»øö________½ĒČż½ĒŠĪ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĢåÓżæĪÉĻ£¬ĄĻŹ¦²āĮæĢųŌ¶³É¼ØµÄÖ÷ŅŖŅĄ¾ŻŹĒ£Ø £©
A. “¹Ļ߶Ī×ī¶Ģ B. Į½µćÖ®¼ä£¬Ļ߶Ī×ī¶Ģ
C. Ę½ŠŠĻß¼äµÄ¾ąĄėĻąµČ D. Į½µćČ·¶ØŅ»ĢõÖ±Ļß
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ¾ŲŠĪABCDÖŠ£¬AB=3£¬AD=4£¬¶ÆµćQ“ÓµćA³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶Č£¬ŃŲABĻņµćBŅĘ¶Æ£»Ķ¬Ź±µćP“ÓµćB³ö·¢£¬ČŌŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶Č£¬ŃŲBCĻņµćCŅĘ¶Æ£¬Į¬½ÓQP£¬QD£¬PD£®ČōĮ½øöµćĶ¬Ź±ŌĖ¶ÆµÄŹ±¼äĪŖxĆė£Ø0£¼x”Ü3£©£¬½ā“šĻĀĮŠĪŹĢā£ŗ
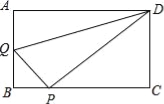

£Ø1£©Éč”÷QPDµÄĆ껿ĪŖS£¬ÓĆŗ¬xµÄŗÆŹż¹ŲĻµŹ½±ķŹ¾S£»µ±xĪŖŗĪÖµŹ±£¬SÓŠ×ī“óÖµ£æ²¢Ēó³ö×īŠ”Öµ£»
£Ø2£©ŹĒ·ń“ęŌŚxµÄÖµ£¬Ź¹µĆQP”ĶDP£æŹŌĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»ŌŖ¶ž“Ī·½³Ģx2©2x©3=0µÄ¶ž“ĪĻīĻµŹż”¢Ņ»“ĪĻīĻµŹż”¢³£ŹżĻī·Ö±šŹĒ£Ø £©
A. 1£¬2£¬©3 B. 1£¬©2£¬3 C. 1£¬2£¬3 D. 1£¬©2£¬©3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄ·½³Ģ£¬£Ø1£©ax2+bx+c=0£»£Ø2£©x2-4x=0£»£Ø3£©1+£Øx-1£©£Øx+1£©=0£»£Ø4£©3x2=0ÖŠ£¬Ņ»ŌŖ¶ž“Ī·½³ĢµÄøöŹżĪŖ£Ø”” ””£©øö£®
A. 1 B. 2 C. 3 D. 4
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com