
分析 (1)根据因式分解法,可得方程的解;
(2)根据配方法,可得方程的解;
(3)根据因式分解法,可得方程的解;
(4)根据因式分解法,可得方程的解.
解答 解:(1)因式分解,得
(x-1)(x+4)=0.
于是,得
x-1=0或x+4=0,
x1=1,x2=-4;
(2)移项,得
2x2-4x=1,
二次项系数化为1,得
x2-2x=$\frac{1}{2}$,
配方,得
(x-1)2=$\frac{3}{2}$,
开方,得
x-1=±$\frac{\sqrt{6}}{2}$,
x1=$\frac{2+\sqrt{6}}{2}$,x2=$\frac{2-\sqrt{6}}{2}$;
(3)移项,得
3x2-5x-2=0.
因式分解,得
(3x+1)(x-2)=0,
于是,得
3x+1=0,或x-2=0,
x1=-$\frac{1}{3}$,x2=2;
(4)移项,得
4x(2x-1)+(2x-1)=0.
因式分解,得
(2x-1)(4x+1)=0.
于是得
2x-1=0或4x+1=0.
x1=$\frac{1}{2}$,x2=-$\frac{1}{4}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
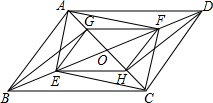 如图,在?ABCD中,AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,BG⊥AC于点G,DH⊥AC于点H,连接EH、HF、FG、GE,那么四边形EHFG是平行四边形吗?请说明理由.
如图,在?ABCD中,AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,BG⊥AC于点G,DH⊥AC于点H,连接EH、HF、FG、GE,那么四边形EHFG是平行四边形吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{{a}^{2}b}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{x{\;}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
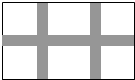 学校课外生物小组的试验园地是长20米宽15米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为252平方米,求小道的宽.
学校课外生物小组的试验园地是长20米宽15米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为252平方米,求小道的宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
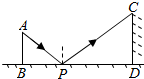 如图,是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,求该古城墙的高度.
如图,是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,求该古城墙的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com