
【题目】用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形.
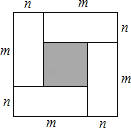
(1)根据图形写出一个代数恒等式: ;
(2)已知3m+n=9,mn=6,试求3m﹣n的值;
(3)若m+n=1,求m2+n2的最小值.
【答案】(1)(m﹣n)2=(m+n)2﹣4mn;(2)45;(3)m2+n2的最小值为![]() .
.
【解析】
(1)直接用阴影正方形边长的平方可求阴影面积,用大正方形面积减四个小长方形的面积可求阴影面积,可得等量关系;
(2)先根据完全平方公式变形,然后代入计算;
(3)由m2+n2=(1-n)2+n2=2(n-![]() )2+
)2+![]() ≥
≥![]() ,可求m2+n2的最小值.
,可求m2+n2的最小值.
(1)∵直接用阴影正方形边长的平方可求阴影面积=(m﹣n)2,用大正方形面积减四个小长方形的面积可求阴影面积=(m+n)2﹣4mn,
∴(m﹣n)2=(m+n)2﹣4mn;
(2)∵(3m﹣n)2=(3m+n)2﹣6mn,
∴(3m﹣n)2=81﹣36=45;
(3)∵m+n=1,
∴m=1﹣n,
∴m2+n2=(1﹣n)2+n2=1+2n2﹣2n=2(n﹣![]() )2+
)2+![]() ≥
≥![]() ,
,
∴m2+n2的最小值为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一些相同的房间需要粉刷墙面.一天3名一级技工去粉刷8个房间,结果其中有40m2墙面未来得及粉刷;同样时间内5名二级技工刚好粉刷了10个房间,每名一级技工比二级技工一天多粉刷20m2墙面.
(1)一级技工和二级技工每人每天各粉刷多少墙面?
(2)现有若干间这样的房间需要在规定的时间内粉刷完墙面,若安排一名一级技工单独粉刷,可比规定时间提前1天完成;若安排一名二级技工单独完成,到规定时间还有4间房间没粉刷.需要粉刷的房间一共有多少间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图中网格上按要求画出图形,并回答问题:
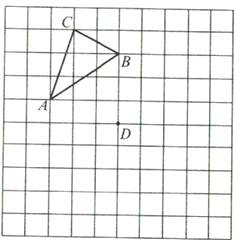
(1)如果将三角形![]() 平移,使得点
平移,使得点![]() 平移到图中点
平移到图中点![]() 位置,点
位置,点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,请画出三角形
,请画出三角形![]() ;
;
(2)画出三角形![]() 关于点
关于点![]() 成中心对称的三角形
成中心对称的三角形![]() .
.
(3)三角形![]() 与三角形
与三角形![]() ______(填“是”或“否”)关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点
______(填“是”或“否”)关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
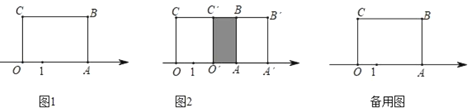
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为 .
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为OABC,移动后的长方形OABC与原长方形OABC重叠部分(如图8中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A表示的数是 .
②设点A的移动距离AA'=x
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA的中点,点E在找段OO'上,且OO'=3OE,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的春季趣味运动会深受学生喜爱,该校体育教师为了了解该次运动会中四个项目的受欢迎程度,随机抽取了部分学生进行问卷调查,被调查学生须从“托球跑、掷飞盘、推小车、鸭子步”四个项目中选择自己最喜欢的一项.
根据调查结果,体育教师绘制了图1和图2两个统计图(均未完成),请根据图1和图2的信息,解答下列问题.
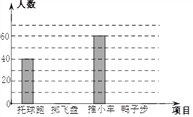
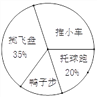
(1)此次共调查了多少名学生?
(2)将条形统计图补充完整.
(3)图2中“鸭子步”所在扇形圆心角为多少度?
(4)若全校有学生1600人,估计该校喜欢“推小车”项目的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中的一个正方形剪开得到图③,图③中共有7个正方形;将图③中的一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2019个图中共有正方形的个数为( ).
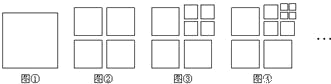
A.6052B.6055C.6058D.6061
查看答案和解析>>
科目:初中数学 来源: 题型:
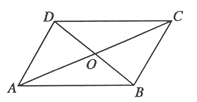
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC=8![]() ,BD=6
,BD=6![]() ,且
,且![]() ,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com