
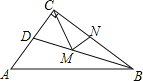
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“校本课程”是学生课外活动的重要内容,某校共有“文学欣赏”、“英语角”、“趣味数学”、“法律普及”这四种校本课程.为了解学生参加“文学欣赏”、“英语角”、“趣味数学”、“法律普及”校本课程(以下分别用A、B、C、D表示)的情况,对学生进行了抽样调查,并将调查情况绘制成两幅统计图(尚不完整). 
请根据以上信息,解答下列问题:
(1)本次抽样调查的学生共有人.
(2)将两幅统计图补充完整;
(3)若该校有4000人,请估计参加法律普及的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
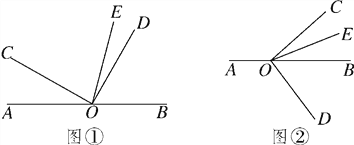
【题目】(12分)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这四边行ABCD中,点M、N分别在AB,CD边上,将四边形ABCD沿MN翻折,使点B、C分别在四边形外部点B1 , C1处,则∠A+∠B1+∠C1+∠D= . 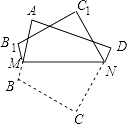
查看答案和解析>>
科目:初中数学 来源: 题型:
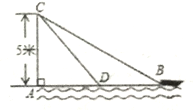
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
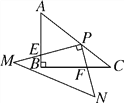
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点的左边,距离原点8个单位长度,点B在原点的右边.
(Ⅰ)求点A,点B对应的数;
(Ⅱ)数轴上点A以每秒1个单位长度出发向左移动,同时点B以每秒3个单位长度的速度向左移动,在点C处追上了点A,求点C对应的数.
(Ⅲ)已知在数轴上点M从点A出发向右运动,速度为每秒1个单位长度,同时点N从点B出发向右运动,速度为每秒2个单位长度,设线段NO的中点为P(O为原点),在运动的过程中,线段![]() 的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
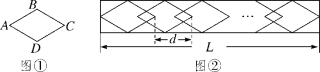
【题目】某工厂沿路护栏的纹饰部分是由若干个和菱形ABCD(如图①)全等的图案组成的,每增加一个菱形,纹饰长度就增加dcm(如图②).已知菱形ABCD的边长为6![]() cm,∠BAD=60°.
cm,∠BAD=60°.
(1)求AC的长;
(2)若d=15cm,纹饰总长度L为3918cm,则需要多少个这样的菱形图案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com