
【题目】将一个三位正整数n各数位上的数字重新排列(含n本身)后,得到新的三位数![]() (a<c),在所有重新排列大的数中,当|a+c﹣2b|最小时,我们称
(a<c),在所有重新排列大的数中,当|a+c﹣2b|最小时,我们称![]() 是n的“天时数”,并规定F(n)=b2﹣ac.当|a+c﹣2b|最大时,我们称
是n的“天时数”,并规定F(n)=b2﹣ac.当|a+c﹣2b|最大时,我们称![]() 是n的“地利数”,并规定G(n)=ac﹣b2.并规定M(n)=
是n的“地利数”,并规定G(n)=ac﹣b2.并规定M(n)=![]() 是n的“人和数”,例如:215可以重新排列为125,152,215,因为|1+5﹣2×2|=2,|1+2﹣2×5|=7,|2+5﹣2×1|=5,且2<5<7,所以125是215的“天时数”F(125)=22﹣1×5=﹣1,152是215的“地利数”,G(152)=1×2﹣52=﹣23,M(215)=
是n的“人和数”,例如:215可以重新排列为125,152,215,因为|1+5﹣2×2|=2,|1+2﹣2×5|=7,|2+5﹣2×1|=5,且2<5<7,所以125是215的“天时数”F(125)=22﹣1×5=﹣1,152是215的“地利数”,G(152)=1×2﹣52=﹣23,M(215)=![]() .
.
(1)计算:F(168),G(168);
(2)设三位自然数s=100x+50+y(1≤x≤9,1≤y≤9,且x,y均为正整数),交换其个位上的数字与百位上的数字得到t,若s﹣t=693,那么我们称s为“厚积薄发数”;请求出所有“厚积薄发数”中M(s)的最大值.
【答案】(1)28,47;(2)![]()
【解析】
(1)将168重新排列为168、186,计算出|1+8﹣2×6|=3、|1+6﹣2×8|=9且3<9可得168的天时数与地利数,再根据天时数和地利数的定义计算可得;
(2)由s=100x+50+y,t=100y+50+x,根据s﹣t=693可得![]() 或
或![]() ,据此得出s的“厚积薄发数”为851或952,再分别求出这两个数的“人和数”,比较大小即可得.
,据此得出s的“厚积薄发数”为851或952,再分别求出这两个数的“人和数”,比较大小即可得.
(1)168重新排列为168、186、618.
∵|1+8﹣2×6|=3、|1+6﹣2×8|=9、|8+6﹣2×1|=12,且3<9<12,∴168是168的天时数,F(168)=62﹣1×8=28;
618是168的地利数,G(618)=6×8﹣12=47.
(2)s=100x+50+y,t=100y+50+x.
∵s﹣t=99x﹣99y=693,∴99(x﹣y)=693,x﹣y=7,x=y+7,∴1≤x≤9,1≤y≤9,∴1≤y+7≤9,∴1≤y≤2,∴![]() 或
或![]() ,∴s的“厚积薄发数”为851或952,当s=851时,可以重新排列为158,185,518.
,∴s的“厚积薄发数”为851或952,当s=851时,可以重新排列为158,185,518.
∵|1+8﹣2×5|=1,|1+5﹣2×8|=10,|5+8﹣2×1|=11,∴158为851的“天时数”,F(851)=52﹣1×8=17;
518为851的“地利数”G(851)=5×8﹣12=39;
则M(851)=![]() ;
;
当s=952时,可以重新排列为529、295、259.
∵|5+9﹣2×2|=10,|2+5﹣2×9|=11,|2+9﹣2×5|=1,∴259为952的“天时数”,F(952)=52﹣2×9=7;
295为952的“地利数”,G(952)=2×5﹣92=﹣71,则M(952)=﹣![]() ;
;
综上,知所有“厚积薄发数”中M(s)的最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点.

(1)求这个二次函数以及直线BC的解析式;
(2)直接写出点A的坐标;
(3)当x为何值时,一次函数的值大于二次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】具备下列条件的两个三角形,可以证明它们全等的是( ).
A.一边和这一边上的高对应相等B.两边和第三边上的中线对应相等
C.两边和其中一边的对角对应相等D.直角三角形的斜边对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从![]() 两水库向甲、乙两地调水,其中甲地需水
两水库向甲、乙两地调水,其中甲地需水![]() 万吨,乙地需水
万吨,乙地需水![]() 万吨,
万吨,![]() 两水库各可调出水
两水库各可调出水![]() 万吨,从
万吨,从![]() 水库到甲地
水库到甲地![]() 千米,到乙地
千米,到乙地![]() 千米;从
千米;从![]() 水库到甲地
水库到甲地![]() 千米,到乙地
千米,到乙地![]() 千米,设计一个调运方案使水的调运总量(单位:万吨千米)尽可能大。
千米,设计一个调运方案使水的调运总量(单位:万吨千米)尽可能大。
查看答案和解析>>
科目:初中数学 来源: 题型:
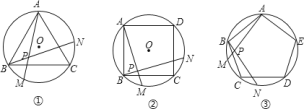
【题目】如图①、②、③,正三角形![]() 、正方形
、正方形![]() 、正五边形
、正五边形![]() 分别是
分别是![]() 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 开始,以相同的速度中
开始,以相同的速度中![]() 上逆时针运动.如图①、②、③,正三角形
上逆时针运动.如图①、②、③,正三角形![]() 、正方形
、正方形![]() 、正五边形
、正五边形![]() 分别是
分别是![]() 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 开始,以相同的速度中
开始,以相同的速度中![]() 上逆时针运动.
上逆时针运动.
(1)求图①中![]() 的度数;
的度数;
(2)图②中,![]() 的度数是________,图③中
的度数是________,图③中![]() 的度数是________;
的度数是________;
(3)根据前面探索,你能否将本题推广到一般的正![]() 边形情况?若能,写出推广问题和结论;若不能,请说明理由.
边形情况?若能,写出推广问题和结论;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加某体育项目训练,为了便于研究,把最后5次的训练成绩分别用实线和虚线连接起来,如图,下面的结论错误的是( )

A. 乙的第2次成绩与第5次成绩相同
B. 第3次测试,甲的成绩与乙的成绩相同
C. 第4次测试,甲的成绩比乙的成绩多2分
D. 在5次测试中,甲的成绩都比乙的成绩高
查看答案和解析>>
科目:初中数学 来源: 题型:
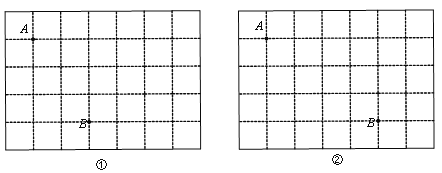
【题目】如图①、图②,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点,图①和图②中的点A、点B都是格点.分别在图①、图②中画出格点C,并满足下面的条件:
(1)在图①中,使∠ABC=90°.此时AC的长度是 .
(2)在图②中,使AB=AC.此时△ABC的边AB上的高是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com