
分析 (1)根据题意可得“全球通”使用者的费用=50元/月+0.4元×通话时间;“神州行”的费用=0.6元×通话时间,进而可得解析式;
(2)此题要分三种情况:①y1=y2 时,②y1>y2 时,③y1<y2 时,分别列出方程或不等式,再解即可.
解答 解:(1)由题意可知y1=50+0.4x,
y2=0.6x,
(2)当y1=y2 时,即50+0.4x=0.6x,解得x=250,
当y1>y2 时,即50+0.4x>0.6x,解得x<250,
当y1<y2 时,即50+0.4x<0.6x,解得x>250,
∴当用户每月通话时间少于250分钟,选“神州行”,
当多于250分钟选“全球通”,
当通话时间为250分钟时,选择哪种方式都一样.
点评 此题主要考查了一次函数的应用,关键是正确理解题意,找出题目中等量关系,列出函数关系式.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
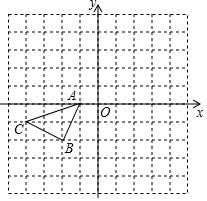 在直角坐标系中,△ABC的三个顶点的位置如图所示:
在直角坐标系中,△ABC的三个顶点的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2<m<-$\frac{2}{3}$ | B. | m>-2 | C. | -2≤m≤-$\frac{2}{3}$ | D. | m<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$x(x+1)=21 | B. | x(x+1)=21 | C. | $\frac{1}{2}$x(x-1)=21 | D. | x(x-1)=21 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是②或③或④.
如图所示,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是②或③或④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (8-6)÷8 | B. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{6}$ | C. | $\frac{1}{6}$÷$\frac{1}{8}$ | D. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
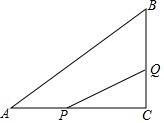 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+1=(26-x)-2 | B. | x+1=(13-x)-2 | C. | x-1=(26-x)+2 | D. | x-1=(13-x)+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com