
 ∠ACB,∠OBC=
∠ACB,∠OBC= ∠ABC,根据三角形的内角和定理求出∠ABC+∠ACB,求出∠OBC+∠OCB,再根据三角形的内角和定理即可求出答案.
∠ABC,根据三角形的内角和定理求出∠ABC+∠ACB,求出∠OBC+∠OCB,再根据三角形的内角和定理即可求出答案.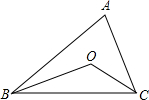 解:∵点O是△ABC内一点,且O到三边的距离相等,
解:∵点O是△ABC内一点,且O到三边的距离相等, ∠ACB,∠OBC=
∠ACB,∠OBC= ∠ABC,
∠ABC, (∠ACB+∠ABC)=59°,
(∠ACB+∠ABC)=59°,

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
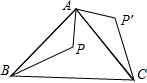 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一点,△ABP绕点A逆时针旋转后与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一点,△ABP绕点A逆时针旋转后与△ACP′重合,如果AP=| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com