
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 不能确定 |
分析 首先根据一元二次方程的定义以及二次根式的意义得出k-1≠0,1-k≥0,那么k<1,再计算根的判别式,然后根据判别式的意义判断根的情况.
解答 解:∵(k-1)x2-$\sqrt{1-k}$x+$\frac{1}{2}$=0是关于x的一元二次方程,
∴k-1≠0,1-k≥0,
∴k<1,
又△=1-k-4×(k-1)×$\frac{1}{2}$=3-3k>0,
∴方程有两个不相等的实数根.
故选A.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义以及二次根式的意义.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
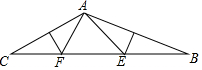 如图,在△ABC中,∠CAB=130°,AB、AC的垂直平分线分别交BC于点E、F则∠EAF等于( )
如图,在△ABC中,∠CAB=130°,AB、AC的垂直平分线分别交BC于点E、F则∠EAF等于( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-$\frac{1}{2}$x | B. | y=-2x | C. | y=2x | D. | y=-x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC=10,BC=16,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=10,BC=16,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )| A. | 5个 | B. | 7个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 cm或5 cm | B. | 3 cm或7 cm | C. | 3 cm | D. | 5 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 40° 或140° | B. | 45°或135° | C. | 50° | D. | 80° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com