
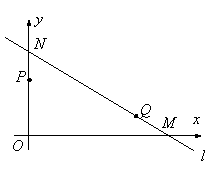
如图, 直线![]() 与
与![]() 轴、
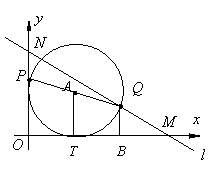
轴、![]() 轴分别交于点M(8,0)点N(0,6),点
轴分别交于点M(8,0)点N(0,6),点![]() 以每秒3个单位长度的速度沿NO由N向O运动,点
以每秒3个单位长度的速度沿NO由N向O运动,点![]() 以每秒5个单位长度的速度沿MN由M向N运动.已知点
以每秒5个单位长度的速度沿MN由M向N运动.已知点![]() 同时出发,且当一点运动到终点时,另一点也随之停止运动,设运动时间为
同时出发,且当一点运动到终点时,另一点也随之停止运动,设运动时间为![]() 秒.
秒.
(1)当四边形PQMO为梯形时,求t的值;
(2)当△PQO为等腰三角形时,求t的值;
(3)在整个运动中,以PQ为直径的圆能否与x轴相切?若能,请求出运动时间t;若不能,请说明理由.
 |
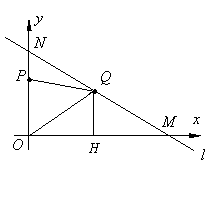
(1)当PQ∥AB时,当四边形PQMO为梯形
此时有![]() ………(1分)
………(1分)
即![]() ,解得:t=1.
,解得:t=1.
所以,当t=1秒时,四边形PQMO为梯形………(3分)
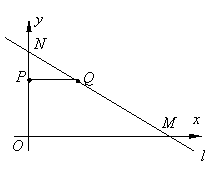
(2)P点的坐标为(0,6-3t),
Q点的坐标为(8-4t, 3t)…………(4分)
![]() 为等腰三角形
为等腰三角形
当PO=OQ时,作OH⊥x轴于点H
在Rt△OQH中,有![]()
此时方程无实数根,故此种情况不存在. ……(5分)
当PQ=OQ时,此时Q在OP的垂直平分线上
所以P点的纵坐标是Q点纵坐标的2倍
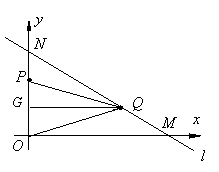 即有
即有![]() ,
,![]()
当![]() 秒时,
秒时,![]() 为等腰三角形. ……(7分)
为等腰三角形. ……(7分)
当PO=PQ时,作OG⊥y轴于点G
在Rt△PGQ中,有![]()
此时方程无实数根,故此种情况不存在. ……(8分)
(3) 若以PQ为直径的⊙A与x轴相切点T,连接AT,作QB⊥x轴于点B,则AT=R=![]() (OP+QB)=
(OP+QB)=![]() PQ ……(9分)
PQ ……(9分)
即OP+QB=PQ
所以![]() …(11分)
…(11分)
解得:![]()
所以当![]() 时,以PQ为直径的圆与x轴相切…………………………………(12分)
时,以PQ为直径的圆与x轴相切…………………………………(12分)


科目:初中数学 来源: 题型:
如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B,A,且A,B两点的坐标分别为A
轴分别交于点B,A,且A,B两点的坐标分别为A![]() ,B
,B![]() .
.
(1)请求出直线![]() 的函数解析式;
的函数解析式;
在x轴上是否存在这样的点C,使△ABC为等腰三角形?请求出点C的坐标(不需要具体过程),并在坐标系中标出点C的大致位置;
查看答案和解析>>
科目:初中数学 来源: 题型:
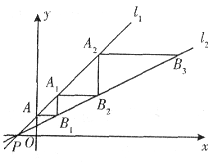
如图,直线![]() 平行于直线
平行于直线![]() ,且与直线
,且与直线![]() 相交于点P(-1,0)。
相交于点P(-1,0)。
(1)求直线![]() 、
、![]() 的解析式;
的解析式;
(2)直线![]() 与
与![]() 轴交于点A,一动点C从点A出发,先沿平行于
轴交于点A,一动点C从点A出发,先沿平行于![]() 轴的方向运动,到达直线
轴的方向运动,到达直线![]() 上的点
上的点![]() 处后,改为垂直于
处后,改为垂直于![]() 轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点
轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点![]() 处后,又改为垂直于
处后,又改为垂直于![]() 轴的方向运动,到达直线
轴的方向运动,到达直线![]() 上的点
上的点![]() 处后,仍沿平行于
处后,仍沿平行于![]() 轴的方向运动,……,照此规律运动,动点C依次经过点
轴的方向运动,……,照此规律运动,动点C依次经过点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…。
,…。
①求点![]() ,
,![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
②请你通过归纳得出点![]() 、
、![]() 的坐标;并求当动点C到达
的坐标;并求当动点C到达![]() 处时,运动的总路径的长。
处时,运动的总路径的长。
查看答案和解析>>
科目:初中数学 来源:2011届江西省中考数学预测试卷三解析版 题型:解答题
如图,直线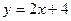 与
与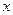 轴、
轴、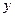 轴分别交于A、B两点,把△OAB绕点O顺时针旋转90°得到△OCD.
轴分别交于A、B两点,把△OAB绕点O顺时针旋转90°得到△OCD.
⑴在图中画出△OCD;
⑵求经过A、B、D三点的抛物线的解析式;
⑶点P在抛物线对称轴上运动
①当直线CP把△OCD分成面积相等的两部分时,试求出点P的坐标;
②是否存在点P,使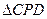 为直角三角形,若存在,请求出点
为直角三角形,若存在,请求出点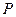 的坐标;如果不存在,请
的坐标;如果不存在,请
说明理由.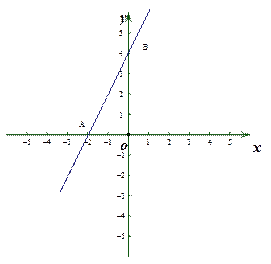
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江临安於潜第一初级中学九年级上期末综合考试数学试卷(一)(解析版) 题型:解答题
(本题12分)
如图,直线 与
与 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.
动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.
动直线EF从 轴开始以每秒1个长度单位的速度向上平行移动(即EF∥
轴开始以每秒1个长度单位的速度向上平行移动(即EF∥ 轴),并且分别与
轴),并且分别与 轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.

(1)当t=1秒时,求梯形OPFE的面积;
(2)t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3)设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市西城区(北区)九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,直线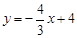 与
与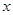 轴、
轴、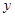 轴分别交于
轴分别交于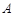 、
、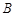 两点,△
两点,△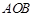 绕点
绕点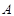 顺时针旋转90后得到△
顺时针旋转90后得到△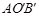 ,则点
,则点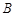 的对应点
的对应点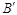 坐标为
坐标为

A.(3,4) B.(7,4)
C.(7,3) D.(3,7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com