
【题目】某数学活动小组在做角的拓展图形练习时,经历了如下过程:
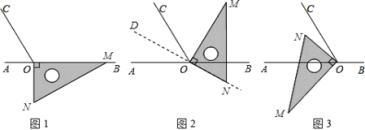
(1)操作发现:点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() 将一直角三角板的直角顶点放在点
将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方,如图:将图1中的三角板绕点
的下方,如图:将图1中的三角板绕点![]() 旋转,当直角三角板的
旋转,当直角三角板的![]() 边在
边在![]() 的内部,且恰好平分
的内部,且恰好平分![]() 时,如图2.则下列结论正确的是 (填序号即可).
时,如图2.则下列结论正确的是 (填序号即可).
①![]() ②
②![]() ③
③![]() 平分
平分![]() ④
④![]() 的平分线在直线
的平分线在直线![]() 上
上
(2)数学思考:同学们在操作中发现,当三角板绕点![]() 旋转时,如果直角三角板的
旋转时,如果直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方,那么
在直线AB的下方,那么![]() 与
与![]() 的差不变,请你说明理由;如果直角三角板的
的差不变,请你说明理由;如果直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部,那么
的内部,那么![]() 与
与![]() 的和不变,请直接写出
的和不变,请直接写出![]() 与
与![]() 的和,不要求说明理由.
的和,不要求说明理由.
(3)类比探索:三角板绕点![]() 继续旋转,当直角三角板的
继续旋转,当直角三角板的![]() 边在
边在![]() 的内部时,如图3,求
的内部时,如图3,求![]() 与
与![]() 相差多少度?为什么?
相差多少度?为什么?
【答案】(1)①②④;(2)如果直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方,那么
在直线AB的下方,那么![]() 与
与![]() 的差不变,理由见解析;如果直角三角板的
的差不变,理由见解析;如果直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部,那么
的内部,那么![]() 与
与![]() 的和不变,
的和不变,![]() +
+![]() =30°;③30°.
=30°;③30°.
【解析】
(1)利用角平分线的定义结合直角三角板的内角度数即可分别判断得出答案;
(2)当直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方时根据∠COM=120°-∠BOM,∠BON=90°-∠BOM,可得出结果;当直角三角板的
在直线AB的下方时根据∠COM=120°-∠BOM,∠BON=90°-∠BOM,可得出结果;当直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部时,∠COM+∠BON=∠BOC-∠MON,可得出结果;
的内部时,∠COM+∠BON=∠BOC-∠MON,可得出结果;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,然后作差即可.
解:(1)∵![]() ,
,![]() 平分
平分![]() ,∴
,∴![]() ,故①正确;
,故①正确;
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,故②正确;
,故②正确;
∵![]() ,
,![]() ,∴
,∴![]() 不平分
不平分![]() ,故③错误;
,故③错误;
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() 的平分线在直线
的平分线在直线![]() 上,故④正确;
上,故④正确;
故答案为:①②④.
(2)![]() 与
与![]() 的差不变.理由如下:当直角三角板的
的差不变.理由如下:当直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方时,
在直线AB的下方时,
∵∠COM=∠BOC-∠COM=120°-∠BOM,
∠BON=∠MON-∠BOM=90°-∠BOM,
∴∠COM-∠BON=120°-90°=30°;![]() 与
与![]() 的和不变,其和为30°.理由如下:当直角三角板的
的和不变,其和为30°.理由如下:当直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部时,∠COM+∠BON=∠BOC-∠MON=120°-90°=30°.
的内部时,∠COM+∠BON=∠BOC-∠MON=120°-90°=30°.
(3)∵![]() ,
,![]() ,
,
∴![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】一副三角尺按照如图所示摆放在量角器上,边![]() 与量角器
与量角器![]() 刻度线重合,边
刻度线重合,边![]() 与量角器
与量角器![]() 刻度线重合,将三角尺
刻度线重合,将三角尺![]() 绕量角器中心点
绕量角器中心点![]() 以每秒
以每秒![]() 的速度顺时针旋转,当边
的速度顺时针旋转,当边![]() 与
与![]() 刻度线重合时停止运动.设三角尺
刻度线重合时停止运动.设三角尺![]() 的运动时间为
的运动时间为![]() (秒)
(秒)
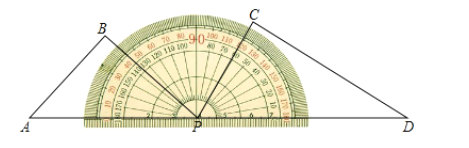
(1)当![]() 秒时,边
秒时,边![]() 经过的量角器刻度线对应的度数为_ ;
经过的量角器刻度线对应的度数为_ ;
(2)![]() 秒时,边
秒时,边![]() 平分
平分![]() ;
;
(3)若在三角尺![]() 开始旋转的同时,三角尺
开始旋转的同时,三角尺![]() 也绕点
也绕点![]() 以每秒
以每秒![]() 的速度逆时针旋转,当三角尺
的速度逆时针旋转,当三角尺![]() 停止旋转时,三角尺
停止旋转时,三角尺![]() 也停止旋转,
也停止旋转,
①当![]() 为何值时,边
为何值时,边![]() 平分
平分![]() ;
;
![]() .若存在,请求出
.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD∶AB=__________时,四边形MENF是正方形(只写结论,不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仔细观察如图所示的折纸过程,然后回答下列问题:

(1)![]() 的度数为__________;
的度数为__________;
(2)![]() 与
与![]() 有何数量关系:______;
有何数量关系:______;
(3)![]() 与
与![]() 有何数量关系:__________;
有何数量关系:__________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E为边AB上一点,且AE=![]() AB,EF⊥EC,连接BF.
AB,EF⊥EC,连接BF.
(1)求证:△AEF∽△BCE;
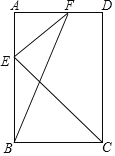
(2)若AB=3![]() ,BC=3,求线段FB的长.
,BC=3,求线段FB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】透明的口袋里装有3个球,这3个球分别标有数字1、2、3,这些球除了数字外都相同。
(1)如果从袋中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?(3分)
(2)小明和小东玩摸球游戏,游戏规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小东随机摸出一个球,记下球的数字.谁摸出的球的数字大,谁获胜.现请你利用树状图或列表的方法分析游戏规则对双方是否公平?并说明理由。(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年元旦期间,某商场打出促销广告,如表所示.
优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com