
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD= ![]() .
. 
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
【答案】
(1)解:∵AB与圆O相切,
∴OD⊥AB,
在Rt△BDO中,BD=2,tan∠BOD= ![]() ,
,
∴OD=3;
(2)解:连接OE,

∵AE=OD=3,AE∥OD,
∴四边形AEOD为平行四边形,
∴AD∥EO,
∵DA⊥AE,
∴OE⊥AC,
又∵OE为圆的半径,
∴AE为圆O的切线
(3)解:∵OD∥AC,
∴ ![]() ,即
,即 ![]() ,
,
∴AC=7.5,
∴EC=AC﹣AE=7.5﹣3=4.5,
∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG
= ![]() ×2×3+
×2×3+ ![]() ×3×4.5﹣
×3×4.5﹣ ![]()
=3+ ![]() ﹣
﹣ ![]()
= ![]() .
.
【解析】(1)由AB为圆O的切线,利用切线的性质得到OD垂直于AB,在直角三角形BDO中,利用锐角三角函数定义,根据tan∠BOD及BD的值,求出OD的值即可;(2)连接OE,由AE=OD=3,且OD与AE平行,利用一组对边平行且相等的四边形为平行四边形,根据平行四边形的对边平行得到OE与AD平行,再由DA与AE垂直得到OE与AC垂直,即可得证;(3)阴影部分的面积由三角形BOD的面积+三角形ECO的面积﹣扇形DOF的面积﹣扇形EOG的面积,求出即可.
【考点精析】本题主要考查了扇形面积计算公式的相关知识点,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表: 抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题: 
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 , 表示C组扇形的圆心角θ的度数为度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市举行的中学生安全知识竞赛中共有20道题.每一题答对得5分,答错或不答都扣3分.
(1)小李考了60分,那么小李答对了多少道题?
(2)小王获得二等奖(75~85分),请你算算小王答对了几道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.

(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x-k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象解决下列问题:
(1)分别求出y甲,y乙与x的函数关系式;
(2)现厂家分配该商品给甲、乙两商场共计1200件,当甲、乙商场售完这批商品,厂家可获得总利润为1080元,问厂家如何分配这批商品?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,∠C=72°,∠ABC的平分线交AC于D,则图中共有等腰三角形( )

A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,已知△ABC,以AB,AC为边分别向△ABC外作等边△ABD和等边△ACE,连结BE,CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;
(2)如图2,利用(1)中的方法解决如下问题:在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,求BD的长.
(3)如图3,四边形ABCD中,∠CAB=90°,∠ADC=∠ACB=α,tanα= ![]() ,CD=5,AD=12,求BD的长.
,CD=5,AD=12,求BD的长.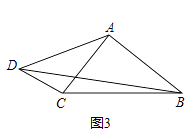
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)若(m,n)是“相伴数对”,其中m≠0,求![]() ;
;
(3)若(m,n)是“相伴数对”,求代数式m﹣![]() ﹣[4m﹣2(3n﹣1)]的值.
﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com