
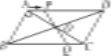
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓθABCD÷–Θ§Ε‘Ϋ«œΏACΓΔBDœύΫΜ”ΎΒψOΘ§ABΓΆACΘ§ABΘΫ3cmΘ§BCΘΫ5cm.ΒψP¥”AΒψ≥ωΖΔ―ΊADΖΫœρ‘»ΥΌ‘ΥΕ·Θ§ΥΌΕ»ΈΣ1cm/s.Ν§ΫαPO≤Δ―”≥ΛΫΜBC”ΎΒψQΘ§…η‘ΥΕ· ±ΦδΈΣt(0ΘΦtΘΦ5)Θ°
(1)Β±tΈΣΚΈ÷Β ±Θ§ΥΡ±Ώ–ΈABQP «ΤΫ––ΥΡ±Ώ–ΈΘΩ
(2)…ηΥΡ±Ώ–ΈOQCDΒΡΟφΜΐΈΣy(cm2)Θ§«σy”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
(3) «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧtΘ§ ΙΒψO‘ΎœΏΕΈAPΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘΩ»τ¥φ‘ΎΘ§«σ≥ωtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
 ΓΓΓΓ
ΓΓΓΓ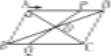 ±Η”ΟΆΦ
±Η”ΟΆΦ
ΓΨ¥πΑΗΓΩΘ®1Θ©Β±tΘΫ![]() ±Θ§ΥΡ±Ώ–ΈABQP «ΤΫ––ΥΡ±Ώ–ΈΘ®2Θ©yΘΫ
±Θ§ΥΡ±Ώ–ΈABQP «ΤΫ––ΥΡ±Ώ–ΈΘ®2Θ©yΘΫ![]() tΘΪ3Θ®3Θ©¥φ‘ΎΘ§Β±tΘΫ
tΘΪ3Θ®3Θ©¥φ‘ΎΘ§Β±tΘΫ![]() ±Θ§ΒψO‘ΎœΏΕΈAPΒΡ¥Ι÷±ΤΫΖ÷œΏ…œ
±Θ§ΒψO‘ΎœΏΕΈAPΒΡ¥Ι÷±ΤΫΖ÷œΏ…œ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίASA÷ΛΟςΓςAPOΓ’ΓςCQOΘ§‘ΌΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ ΒΟ≥ωAPΘΫCQΘΫtΘ§‘ρBQΘΫ5Θ≠tΘ§‘ΌΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ≈–Ε®Ε®άμΩ…÷ΣΒ±APΓΈBQΘ§APΘΫBQ ±Θ§ΥΡ±Ώ–ΈABQP «ΤΫ––ΥΡ±Ώ–ΈΘ§Φ¥tΘΫ5Θ≠tΘ§«σ≥ωtΒΡ÷ΒΦ¥Ω…«σΫβΘΜ
Θ®2Θ©ΙΐAΉςAHΓΆBC”ΎΒψHΘ§ΙΐOΉςOGΓΆBC”ΎΒψGΘ§ΗυΨίΙ¥Ι…Ε®άμ«σ≥ωACΘΫ4Θ§”…RtΓςABCΒΡΟφΜΐΦΤΥψΩ…«σΒΟAHΘΫ![]() Θ§άϊ”Ο»ΐΫ«–Έ÷–ΈΜœΏΕ®άμΩ…ΒΟOG=
Θ§άϊ”Ο»ΐΫ«–Έ÷–ΈΜœΏΕ®άμΩ…ΒΟOG=![]() Θ§‘ΌΗυΨίΥΡ±Ώ–ΈOQCDΒΡΟφΜΐy= SΓςOCDΘΪSΓςOCQΘΫ
Θ§‘ΌΗυΨίΥΡ±Ώ–ΈOQCDΒΡΟφΜΐy= SΓςOCDΘΪSΓςOCQΘΫ![]() OCΓΛCDΘΪ
OCΓΛCDΘΪ![]() CQΓΛOGΘ§¥ζ»κ ΐ÷ΒΦΤΥψΦ¥Ω…ΒΟy”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
CQΓΛOGΘ§¥ζ»κ ΐ÷ΒΦΤΥψΦ¥Ω…ΒΟy”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©»γΆΦ2Θ§»τOE «APΒΡ¥Ι÷±ΤΫΖ÷œΏΘ§Ω…ΒΟAEΘΫ![]() APΘΫ
APΘΫ![]() Θ§ΓœAEOΘΫ90ΓψΘ§ΗυΨίΙ¥Ι…Ε®άμΩ…ΒΟAE2ΘΪOE2ΘΫAO2Θ§”…(2)÷ΣΘΚAOΘΫ2Θ§OEΘΫ
Θ§ΓœAEOΘΫ90ΓψΘ§ΗυΨίΙ¥Ι…Ε®άμΩ…ΒΟAE2ΘΪOE2ΘΫAO2Θ§”…(2)÷ΣΘΚAOΘΫ2Θ§OEΘΫ![]() Θ§Ν–≥ωΙΊ”ΎtΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…«σ≥ωtΒΡ÷Β.
Θ§Ν–≥ωΙΊ”ΎtΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…«σ≥ωtΒΡ÷Β.
(1)ΓΏΥΡ±Ώ–ΈABCD «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύOAΘΫOCΘ§ADΓΈBCΘ§
ΓύΓœPAOΘΫΓœQCO.
”÷ΓΏΓœAOPΘΫΓœCOQΘ§
ΓύΓςAPOΓ’ΓςCQOΘ§
ΓύAPΘΫCQΘΫt.
ΓΏBCΘΫ5Θ§
ΓύBQΘΫ5Θ≠t.
ÿAPøBQȧ
Β±APΘΫBQ ±Θ§ΥΡ±Ώ–ΈABQP «ΤΫ––ΥΡ±Ώ–ΈΘ§
Φ¥tΘΫ5Θ≠tΘ§ΓύtΘΫ![]() Θ§
Θ§
ΓύΒ±tΘΫ![]() ±Θ§ΥΡ±Ώ–ΈABQP «ΤΫ––ΥΡ±Ώ–ΈΘΜ
±Θ§ΥΡ±Ώ–ΈABQP «ΤΫ––ΥΡ±Ώ–ΈΘΜ
(2) ΆΦ1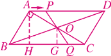
»γΆΦ1Θ§ΙΐAΉςAHΓΆBC”ΎΒψHΘ§ΙΐOΉςOGΓΆBC”ΎΒψG.
‘ΎRtΓςABC÷–Θ§ΓΏABΘΫ3Θ§BCΘΫ5Θ§ΓύACΘΫ4Θ§
ΓύCOΘΫ![]() ACΘΫ2Θ§
ACΘΫ2Θ§
SΓςABCΘΫ![]() ABΓΛACΘΫ
ABΓΛACΘΫ![]() BCΓΛAHΘ§
BCΓΛAHΘ§
Γύ3ΓΝ4ΘΫ5AHΘ§
ΓύAHΘΫ![]() .
.
ΓΏAHΓΈOGΘ§OAΘΫOCΘ§
ΓύGHΘΫCGΘ§
ΓύOGΘΫ![]() AHΘΫ
AHΘΫ![]() Θ§
Θ§
ΓύyΘΫSΓςOCDΘΪSΓςOCQΘΫ![]() OCΓΛCDΘΪ
OCΓΛCDΘΪ![]() CQΓΛOGΘ§
CQΓΛOGΘ§
ΓύyΘΫ![]() ΓΝ2ΓΝ3ΘΪ
ΓΝ2ΓΝ3ΘΪ![]() ΓΝtΓΝ
ΓΝtΓΝ![]() ΘΫ
ΘΫ![]() tΘΪ3ΘΜ
tΘΪ3ΘΜ
ΓΓ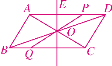 ΆΦ2
ΆΦ2
(3)¥φ‘ΎΘ°
»γΆΦ2Θ§ΓΏOE «APΒΡ¥Ι÷±ΤΫΖ÷œΏΘ§
ΓύAEΘΫ![]() APΘΫ
APΘΫ![]() Θ§ΓœAEOΘΫ90ΓψΘ§
Θ§ΓœAEOΘΫ90ΓψΘ§
”…(2)÷ΣΘΚAOΘΫ2Θ§OEΘΫ![]() Θ§
Θ§
”…Ι¥Ι…Ε®άμΒΟΘΚAE2ΘΪOE2ΘΫAO2Θ§
Γύ(![]() t)2ΘΪ(
t)2ΘΪ(![]() )2ΘΫ22Θ§
)2ΘΫ22Θ§
ΓύtΘΫ![]() ΜρΘ≠
ΜρΘ≠![]() (…α»Ξ)Θ§
(…α»Ξ)Θ§
ΓύΒ±tΘΫ![]() ±Θ§ΒψO‘ΎœΏΕΈAPΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ°
±Θ§ΒψO‘ΎœΏΕΈAPΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ°
Ι ¥πΑΗΈΣΘΚΘ®1Θ©Β±tΘΫ![]() ±Θ§ΥΡ±Ώ–ΈABQP «ΤΫ––ΥΡ±Ώ–ΈΘ®2Θ©yΘΫ
±Θ§ΥΡ±Ώ–ΈABQP «ΤΫ––ΥΡ±Ώ–ΈΘ®2Θ©yΘΫ![]() tΘΪ3Θ®3Θ©¥φ‘ΎΘ§Β±tΘΫ
tΘΪ3Θ®3Θ©¥φ‘ΎΘ§Β±tΘΫ![]() ±Θ§ΒψO‘ΎœΏΕΈAPΒΡ¥Ι÷±ΤΫΖ÷œΏ…œ.
±Θ§ΒψO‘ΎœΏΕΈAPΒΡ¥Ι÷±ΤΫΖ÷œΏ…œ.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫ––ΥΡ±Ώ–ΈABCD÷–Θ§EΓΔFΖ÷±π «±ΏBCΓΔAD…œΒΡΒψΘ§”–œ¬Ν–ΧθΦΰΘΚ
ΔΌAEΓΈCFΘΜΔΎBEΘΫFDΘΜΔέΓœ1ΘΫΓœ2ΘΜΔήAEΘΫCF.
»τ“ΣΧμΦ”Τδ÷–“ΜΗωΧθΦΰΘ§ ΙΥΡ±Ώ–ΈAECF“ΜΕ® «ΤΫ––ΥΡ±Ώ–ΈΘ§‘ρΧμΦ”ΒΡΧθΦΰΩ…“‘ «(ΓΓ ΓΓ)

A. ΔΌΔΎΔέΔή B. ΔΌΔΎΔέ C. ΔΎΔέΔή D. ΔΌΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ2Θ§H‘ΎCDΒΡ―”≥ΛœΏ…œΘ§ΥΡ±Ώ–ΈCEFH“≤ΈΣ’ΐΖΫ–ΈΘ§‘ρΓςDBFΒΡΟφΜΐΈΣ Θ° 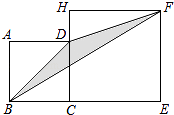
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΗω≤ΜΆΗΟςΒΡ¥ϋ÷–ΉΑ”–20Ηω÷Μ”–―’…Ϊ≤ΜΆ§ΒΡ«ρΘ§Τδ÷–5ΗωΜΤ«ρΘ§8ΗωΚΎ«ρΘ§7ΗωΚλ«ρ.
Θ®1Θ©«σ¥”¥ϋ÷–Οΰ≥ω“ΜΗω«ρ «ΜΤ«ρΒΡΗ≈¬ ΘΜ
Θ®2Θ©œ÷¥”¥ϋ÷–»Γ≥ω»τΗ…ΗωΚΎ«ρΘ§ΫΝ‘»ΚσΘ§ Ι¥”¥ϋ÷–Οΰ≥ω“ΜΗωΚΎ«ρΒΡΗ≈¬ «![]() Θ§«σ¥”¥ϋ÷–»Γ≥ωΚΎ«ρΒΡΗω ΐΘ°
Θ§«σ¥”¥ϋ÷–»Γ≥ωΚΎ«ρΒΡΗω ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύœ¬Ν–ΆΦ–Έ÷–Θ§Φ» «÷αΕ‘≥ΤΆΦ–ΈΘ§”÷ «÷––ΡΕ‘≥ΤΆΦ–ΈΒΡ «Θ® Θ©
A. ÷±Ϋ«»ΐΫ«–Έ
÷±Ϋ«»ΐΫ«–Έ
B. ’ΐΈε±Ώ–Έ
’ΐΈε±Ώ–Έ
C. ’ΐΖΫ–Έ
’ΐΖΫ–Έ
D. ΤΫ––ΥΡ±Ώ–Έ
ΤΫ––ΥΡ±Ώ–Έ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≥ΛΖΫ–Έ![]() ΒΡΗς±ΏΖ÷±πΤΫ––”Ύ
ΒΡΗς±ΏΖ÷±πΤΫ––”Ύ![]() ÷αΜρ
÷αΜρ![]() ÷αΘ§ΈοΧεΦΉΚΆΈοΧε““Ζ÷±π”…Βψ
÷αΘ§ΈοΧεΦΉΚΆΈοΧε““Ζ÷±π”…Βψ![]() Ά§ ±≥ωΖΔΘ§―Ί≥ΛΖΫ–Έ
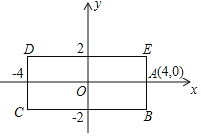
Ά§ ±≥ωΖΔΘ§―Ί≥ΛΖΫ–Έ![]() ΒΡ±ΏΉςΜΖ»Τ‘ΥΕ·Θ°ΈοΧεΦΉΑ¥Ρφ ±’κΖΫœρ“‘2ΗωΒΞΈΜ/Οκ‘»ΥΌ‘ΥΕ·Θ§ΈοΧε““Α¥Υ≥ ±’κΖΫœρ“‘4ΗωΒΞΈΜ/Οκ‘»ΥΌ‘ΥΕ·Θ§‘ρΝΫΗωΈοΧε‘ΥΕ·ΚσΒΡΒΎ2020¥Έœύ”ωΒΊΒψΒΡΉχ±ξ «____Θ°
ΒΡ±ΏΉςΜΖ»Τ‘ΥΕ·Θ°ΈοΧεΦΉΑ¥Ρφ ±’κΖΫœρ“‘2ΗωΒΞΈΜ/Οκ‘»ΥΌ‘ΥΕ·Θ§ΈοΧε““Α¥Υ≥ ±’κΖΫœρ“‘4ΗωΒΞΈΜ/Οκ‘»ΥΌ‘ΥΕ·Θ§‘ρΝΫΗωΈοΧε‘ΥΕ·ΚσΒΡΒΎ2020¥Έœύ”ωΒΊΒψΒΡΉχ±ξ «____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ «Θ® Θ©
A.‘≤ΡΎΫ”’ΐΝυ±Ώ–ΈΒΡ±Ώ≥Λ”κΗΟ‘≤ΒΡΑκΨΕœύΒ»
B.‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§≤ΜΆ§ΒΡΉχ±ξΩ…“‘±μ ΨΆ§“ΜΒψ
C.“Μ‘ΣΕΰ¥ΈΖΫ≥Χax2+bx+c=0Θ®aΓΌ0Θ©“ΜΕ®”– Β ΐΗυ
D.ΫΪΓςABC»ΤAΒψΑ¥Υ≥ ±’κΖΫœρ–ΐΉΣ60ΓψΒΟΓςADEΘ§‘ρΓςABC”κΓςADE≤Μ»ΪΒ»
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ(1)»γΆΦ «”Ο4Ηω»ΪΒ»ΒΡ≥ΛΖΫ–ΈΤ¥≥…ΒΡ“ΜΗωΓΑΜΊ–ΈΓ±’ΐΖΫ–ΈΘ§ΆΦ÷–“θ”Α≤ΩΖ÷ΟφΜΐ”Ο2÷÷ΖΫΖ®±μ ΨΩ…ΒΟ“ΜΗωΒ» ΫΘ§’βΗωΒ» ΫΈΣ_______Θ°
(2)»τ(4x©¹y)2=9Θ§(4x+y)2=169Θ§«σxyΒΡ÷ΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§…δœΏAMΓΈBNΘ§ΒψEΘ§FΘ§D‘Ύ…δœΏAM…œΘ§ΒψC‘Ύ…δœΏBN…œΘ§«“ΓœBCDΘΫΓœAΘ§BEΤΫΖ÷ΓœABFΘ§BDΤΫΖ÷ΓœFBC.
(1)«σ÷ΛΘΚABΓΈCD.
(2)»γΙϊΤΫ––“ΤΕ·CDΘ§Ρ«Ο¥ΓœAFB”κΓœADBΒΡ±»÷Β «ΖώΖΔ…ζ±δΜ·ΘΩ»τ±δΜ·Θ§’“≥ω±δΜ·Ιφ¬…ΘΜ»τ≤Μ±δΘ§«σ≥ω’βΝΫΗωΫ«ΒΡ±»÷ΒΘ°
(3)»γΙϊΓœAΘΫ100ΓψΘ§Ρ«Ο¥‘ΎΤΫ––“ΤΕ·CDΒΡΙΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧΘ§ ΙΓœAEBΘΫΓœBDCΘΩ»τ¥φ‘ΎΘ§«σ≥ω¥Υ ±ΓœAEBΒΡΕ» ΐΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com