
【题目】综合与实践
问题情境:在棱长为1的正方体右侧拼搭若干个棱长小于或等于1的其它正方体,使拼成的立体图形为一个长方体.如图1,是两个棱长为1的正方体搭成的长方体,图2是从上面看这个长方体得到的平面图形,它由两个正方形组成.

操作探究:
(1)如图3是在棱长为1的正方体右侧拼搭了4个棱长小于1的正方体形成的长方体,请画出从上面看这个长方体得到的平面图形;
(2)已知一个长方体是按上述方式拼成的,组成它的正方体不超过10个,且若从上面看这个长方体得到的平面图形由4个正方形组成.
请从A,B两题中任选一题作答,我选择 题.
A.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形)
B.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形,并在所画图形的下方直接写出拼成该长方体所需的正方体的总个数)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2016年12月至1月期间由于空气污染严重,天空中被浓浓的雾霾笼罩着,大多数中小学校为了学生的健康,都不得不停课.针对这一情况有关部门对停课在家的学生家长进行了抽样调查.现将学生家长对这一事件态度的调查结果分为四个等级:“A﹣﹣非常不同意”、“B﹣﹣比校同意”、“C﹣﹣不太同意”、“D﹣﹣非常同意”,并将统计结果绘制成如下两幅不完整的统计图. 请根据以上信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽样调查学生家长的人数为人;
(3)若所调查学生家长的人数为1600人,非常不同意停课的人数为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC、BDEF是面积分别为![]() 、
、![]() 的正方形,点A在x轴上,点F在BC上,点E在反比例函数
的正方形,点A在x轴上,点F在BC上,点E在反比例函数![]() (k>0)的图象上,若
(k>0)的图象上,若![]() ,则k值为( )
,则k值为( )

A. 1 B. ![]() C. 2 D. 4
C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算,当输入x=100时,输出结果为501;当输入x=20时,输出结果为506;如果开始输入的值x为正数,最后输出的结果为656,那么满足条件的x的值最多有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
(1)【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
(2)【类比引申】
如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.
(3)【探究应用】
如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40( ![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E. 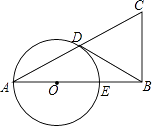
(1)求证:ACAD=ABAE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,CA=CB=2,CD⊥AB于D,点P是线段CD上的一个动点,以点P为直角顶点向下作等腰直角△PBE,
连接DE ,则DE的最小值为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com