已知抛物线C1:y=x2+mx+1的顶点在x轴负半轴上.
(1)求抛物线C1的顶点坐标;
(2)把抛物线C1向下平移若干个单位后,得到抛物线C2,已知C2与x轴的交点为A(1,0)、B,求抛物线C2的函数解析式和B点的坐标;
(3)若P(n,y1)、Q(2,y2)是抛物线C1上的两点,且y1>y2.直接写出实数n的取值范围.
解:(1)∵y=x
2+mx+1的顶点在x轴负半轴上,
∴b
2-4ac=m
2-4=0,x=-

<0,则m>0,
解得:m
1=2,m
2=-2(不合题意舍去),
∴y=x
2+mx+1=x
2+2x+1=(x+1)
2,
∴C
1的顶点坐标为(-1,0);
(2)设C
2的函数关系式为y=(x+1)
2+k,
把A(1,0)代入上式得(1+1)
2+k=0,得k=-4,
∴C
2的函数关系式为y=(x+1)
2-4.
∵抛物线的对称轴为直线x=-1,与x轴的一个交点为A(1,0),
由对称性可知,它与x轴的另一个交点B的坐标为(-3,0);
(3)当x≥-1时,y随x的增大而增大,
当n≥-1时,
∵y
1>y
2,
∴n>2.
当n<-1时,P(n,y
1)的对称点坐标为(-2-n,y
1),且-2-n>-1,
∵y
1>y
2,
∴-2-n>2,
∴n<-4.
综上所述:n>2或n<-4.
分析:(1)由于二次函数y=x
2+mx+1的顶点在x轴负半轴上,那么顶点的纵坐标为0,由此可以确定m.
(2)首先设所求抛物线解析式为y=(x+1)
2+k,然后把A(1,0)代入即可求出k,也就求出了抛物线的解析式;
(3)由于图象C
1的对称轴为直线x=-1,所以知道当x≥-1时,y随x的增大而增大,然后讨论n≥-1和n≤-1两种情况,利用前面的结论即可得到实数n的取值范围.
点评:此题考查了抛物线与x轴交点个数与其判别式的关系以及抛物线平移的性质和抛物线的增减性,熟练掌握二次函数平移的性质是解题关键.

 <0,则m>0,
<0,则m>0,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案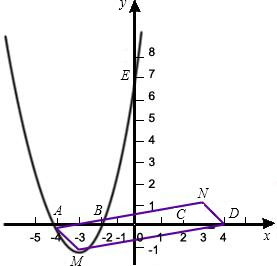 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).