Question

10．已知：矩形ABCD中，AB=10，AD=8，点E是BC边上一个动点，将△ABE沿AE折叠得到△AB′E．
（1）如图1，点G和点H分别是AD和AB′的中点，若点B′在边DC上．
①求GH的长；
②求证：△AGH≌△B′CE；
（2）如图2，若点F是AE的中点，连接B′F，B′F∥AD，交DC于I．
①求证：四边形BEB′F是菱形；
②求B′F的长．

Answer 1

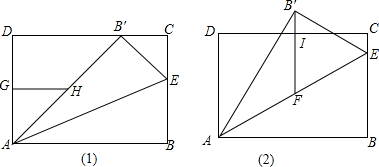
分析 （1）①由折叠的性质可得出AB=AB′，根据矩形的性质可得出∠ADB′=90°，在Rt△ADB′中，利用勾股定理即可得出B′D的长度，再根据中位线的性质即可得出结论；
②由点G为AD的中点可求出AG的长度，通过边与边的关系可得出B′C=4，由此得出B′C=AG，再通过角的计算得出∠AHG=B′EC，由此即可根据全等三角形的判定定理AAS证出△AGH≌△B′CE；
（2）①连接BF，由平行线的性质结合直角三角的中线的性质即可得知△B′EF为等边三角形，根据折叠的性质即可证出四边形BEB′F是菱形；
②由等边三角形和平行线的性质可得出∠BEF=∠B′EF=60°，再由AB=10利用特殊角的三角函数值即可得出结论．

解答 解：（1）①∵将△ABE沿AE折叠得到△AB′E，
∴AB=AB′．
∵四边形ABCD为矩形，
∴∠ADB′=90°，
在Rt△ADB′中，AD=8，AB′=10，
∴B′D=$\sqrt{AB{′}^{2}-A{D}^{2}}$=6．
∵点G和点H分别是AD和AB′的中点，
∴GH为△ADB′的中位线，
∴GH=$\frac{1}{2}$DB′=3．
②证明：∵GH为△ADB′的中位线，
∵GH∥DC，AG=$\frac{1}{2}$AD=4，
∴∠AHG=∠AB′D．
∵∠AB′E=∠ABE=90°，
∴∠AB′D+∠CB′E=90°，
又∵∠CB′E+∠B′EC=90°，
∴∠AHG=B′EC，
∵CD=AB=10，DB′=6，
∴B′C=4=AG．
在△AGH和△B′CE中，有$\left\{\begin{array}{l}{∠AHG=∠B′EC}\\{∠AGH=∠B′CE=90°}\\{B′C=AG}\end{array}\right.$，
∴△AGH≌△B′CE（AAS）．
（2）①证明：连接BF，如图所示．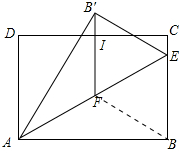
∵将△ABE沿AE折叠得到△AB′E，
∴BF=B′F，∠B′EF=∠BEF，BE=B′E，
∵B′F∥AD，AD∥BC，
∴B′F∥BC，
∴∠B′FE=∠BEF=∠B′EF．
∵∠AB′E=∠ABE=90°，点F为线段AE的中点，
∴B′F=$\frac{1}{2}$AE=FE，
∴△B′EF为等边三角形，
∴B′F=B′E．
∵BF=B′F，BE=B′E，
∴B′F=BF=BE=B′E，
∴四边形BEB′F是菱形．
②∵△B′EF为等边三角形，
∴∠BEF=∠B′EF=60°，
∴BE=AB•cot∠BEF=10×$\frac{\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}$，
∵四边形BEB′F是菱形，
∴B′F=BE=$\frac{10\sqrt{3}}{3}$．

点评 本题考查了折叠的性质、矩形的性质、中位线的性质、全等三角形的判定定理、等边三角形的判定及性质以及菱形的判定定理，解题的关键是：（1）①利用勾股定理求出DB′的长度；②利用全等三角形的判定定理AAS证出△AGH≌△B′CE；（2）①得出△B′EF为等边三角形；②利用特殊角的三角函数值求出BE的长度．本题属于中档题，难度不大，但解题过程稍显繁琐，解决该题型题目时，根据图形的翻折找出相等的边角关系是关键．