
【题目】如图,⊙P在第一象限,半径为3,动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为底边作等腰三角形△ABC,点C在第二象限,且sinA=0.8,点C随点A运动所形成的图形的面积为 .

科目:初中数学 来源: 题型:
【题目】如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于距发射架底部4km处的地面雷达站R(LR=4)测得火箭底部的仰角为43°.1s后,火箭到达B点,此时测得火箭底部的仰角为45.72°.这枚火箭从A到B的平均速度是多少 (结果取小数点后两位)?
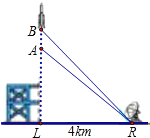
(参考数据:sin43°≈0.682,cos43°≈0.731,tan43°≈0.933,
sin45.72°≈0.716,cos45.72°≈0.698,tan45.72°≈1.025)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读材料,再结合要求回答问题.
【问题情景】
如图①:在四边形ABCD中,AB=AD,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且线段BE,EF,FD满足BE+FD=EF.试探究图中∠EAF与∠BAD之间的数量关系.

【初步思考】
小王同学探究此问题的方法是:延长FD到G,使DG=BE,连结AG.
先证明△ABE≌△ADG,再证明△AEF≌△AGF,
可得出∠EAF与∠BAD之间的数量关系是 .
【探索延伸】
若将问题情景中条件“∠B=∠ADC=90°”改为“∠B+∠D=180°”(如图②),其余条件不变,请判断上述数量关系是否仍然成立,若成立,请证明;若不成立,请说明理由.
【实际应用】
如图③,在某次军事演习中,舰艇甲在指挥中心(O)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处且相距210海里.试求此时两舰艇的位置与指挥中心(O处)形成的夹角∠EOF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①,且∠α=50°,则∠1+∠2= ;
(2)若点P在斜边AB上运动,如图②,则∠α、∠1、∠2之间的关系为 ;
(3)如图③,若点P在斜边BA的延长线上运动(CE<CD),请直接写出∠α、∠1、∠2之间的关系: ;
(4)若点P运动到△ABC形外(只需研究图④情形),则∠α、∠1、∠2之间有何关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)a×a3×(﹣a2)3
(2)(![]() )﹣1+(
)﹣1+(![]() )2×(﹣2)3﹣(π﹣3)0
)2×(﹣2)3﹣(π﹣3)0
(3)(﹣0.25)11×(﹣4)12
(4)(﹣2a2)2×a4﹣(﹣5a4)2.
(5)(x﹣y)6÷(y﹣x)3×(x﹣y)2
(6)314×(﹣![]() )7.
)7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.
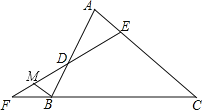
(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年预计建成34个地下调蓄设施,蓄水能力达到140000立方米,将140000用科学记数法表示应为( )
A.14×104 B.1.4×105 C.1.4×106 D.0.14×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com