
【题目】在平面直角坐标系中,点P(2,-4)位于( ).
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
科目:初中数学 来源: 题型:
【题目】(8分)如图,△AOB、△COD是等腰直角三角形,点D在AB上.

(1)求证:△AOC≌△BOD;
(2)若AD=3,BD=1,求CD和△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
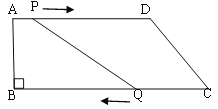
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm, BC=26cm.,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动。规定其中一个动点到达端点时,另一个动点也随之停止运动。从运动开始,使PQ=CD,需要经过多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日孙老师佩戴运动手环进行快走锻炼,两次锻炼后数据如下表.与第一次锻炼相比,孙老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.根据经验已知孙老师第二次锻炼时平均步长减少的百分率小于0.5.
项目 | 第一次锻炼 | 第二次锻炼 | ||
步数(步) | 10000 | ① | ||
平均步长(米/步) | 0.6 | ② | ||
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)求孙老师第二次锻炼时平均步长减少的百分率;
(2)孙老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求孙老师这500米的平均步长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1)![]() 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
![]() 求
求![]() 的值;
的值;
![]() 若CD=2,求BP的长.
若CD=2,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查活动中适合用全面调查的是( )
A.“奔跑吧,兄弟”节目的收视率
B.调查乘坐飞机的旅客是否带了违禁物品
C.某种品牌节能灯的使用寿命
D.了解河北省中学生课外阅读的情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市户籍人口1694000人,则该市户籍人口数据用科学记数法可表示为( )
A.1.694×104人
B.1.694×105人
C.1.694×106人
D.1.694×107人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com