
科目:初中数学 来源: 题型:选择题
 一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
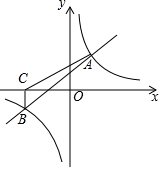 如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.
如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
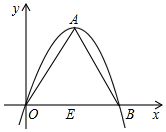 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com