
【题目】如图,在△ABC中,AB=AC,DE∥BC,∠ADE=48°,则下列结论中不正确的是( ) 
A.∠B=48°
B.∠AED=66°
C.∠A=84°
D.∠B+∠C=96°
【答案】B
【解析】解:A、∵DE∥BC,∠ADE=48°, ∴∠B=∠ADE=48°
故A选项正确,但不符合题意;
B、∵AB=AC,
∴∠C=∠B=48°,
∵DE∥BC,
∴∠AED=∠C=48°,
故B选项错误,符合题意;
C、∠A=180°﹣∠B﹣∠C=180°﹣48°﹣48°=84°,故C选项正确,但不符合题意;
D、∠B+∠C=48°+48°=96°,故D选项正确,但不符合题意.
故选:B.
【考点精析】利用平行线的性质和等腰三角形的性质对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角).


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】在我市举行的中学生安全知识竞赛中共有20道题.每一题答对得5分,答错或不答都扣3分.
(1)小李考了60分,那么小李答对了多少道题?
(2)小王获得二等奖(75~85分),请你算算小王答对了几道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,∠C=72°,∠ABC的平分线交AC于D,则图中共有等腰三角形( )

A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,已知△ABC,以AB,AC为边分别向△ABC外作等边△ABD和等边△ACE,连结BE,CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;
(2)如图2,利用(1)中的方法解决如下问题:在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,求BD的长.
(3)如图3,四边形ABCD中,∠CAB=90°,∠ADC=∠ACB=α,tanα= ![]() ,CD=5,AD=12,求BD的长.
,CD=5,AD=12,求BD的长.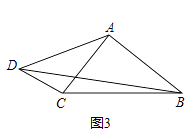
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OM平分∠AOB,直角三角板的直角顶点P在射线OM上移动,两直角边分别与OA、CB相交于点C、D.
(1)问PC与PD相等吗?试说明理由.
(2)若OP=2,求四边形PCOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点M、N分别为ABCD的边CD、AB的中点,连接AM、CN. 
(1)证明:AM=CN;
(2)过点B作BH⊥AM于点H,交CN于点E,连接CH,判断线段CB、CH的数量关系,并说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)若(m,n)是“相伴数对”,其中m≠0,求![]() ;
;
(3)若(m,n)是“相伴数对”,求代数式m﹣![]() ﹣[4m﹣2(3n﹣1)]的值.
﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC,PF⊥CD,垂足分别为点E、F,连接EF,下列结论①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP,其中正确的结论是(请填序号) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com