
【题目】新园小区计划在一块长为20米,宽12米的矩形场地上修建三条互相垂直的长方形甬路(一条橫向、两条纵向,且横向、纵向的宽度比为3:2),其余部分种花草.若要使种花草的面积达到144米2.则横向的甬路宽为_____米.

科目:初中数学 来源: 题型:
【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°.
点拨:如图②,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM.易证:△ABM≌△EBM(SAS),可得AM=EM,∠1=∠2;又AM=MN,则EM=MN,可得∠3=∠4;由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠5,又因为∠2+∠6=120°,所以∠5+∠6=120°,即:∠AMN=60°.
问题:如图③,在正方形A1B1C1D1中,M1是B1C1边上一点(不含端点B1,C1),N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,且A1M1=M1N1.求证:∠A1M1N1=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强对校内外安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型 | 乙型 | |
价格(元/台) | a | b |
有效半径(米/台) | 150 | 100 |
(1)求a、b的值;
(2)若购买该批设备的资金不超过11000元,且要求监控半径覆盖范围不低于1600米,两种型号的设备均要至少买一台,请你为学校设计购买方案,并计算最低购买费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为![]() ,较小的直角边长都为
,较小的直角边长都为![]() ,斜边长都为
,斜边长都为![]() ),大正方形的面积可以表示为
),大正方形的面积可以表示为![]() ,也可以表示为
,也可以表示为![]() ,由此推导出重要的勾股定理:如果直角三角形两条直角边长为
,由此推导出重要的勾股定理:如果直角三角形两条直角边长为![]() ,斜边长为
,斜边长为![]() ,则
,则![]() .
.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在![]() 中,
中,![]() 是
是![]() 边上的高,
边上的高,![]() ,
,![]() ,
,![]() ,设
,设![]() ,求
,求![]() 的值.
的值.
(3)试构造一个图形,使它的面积能够解释![]() ,画在如图4的网格中,并标出字母
,画在如图4的网格中,并标出字母![]() 所表示的线段.
所表示的线段.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(a,0),C(0,c)且满足:(a+6)2+![]() =0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
=0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
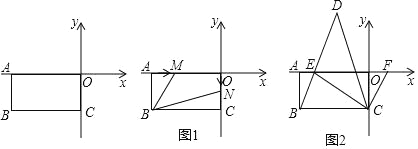
(1)求点B的坐标.
(2)如图1,若点M从点A出发,以2个单位/秒的速度向右运动(不超过点O),点N从原点O出发,以1个单位/秒的速度向下运动(不超过点C),设M、N两点同时出发,在它们运动的过程中,四边形MBNO的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图2,E为x轴负半轴上一点,且∠CBE=∠CEB,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com