
【题目】观察下列关于自然数的等式:
a1:32-12=8×1;
a2:52-32=8×2;
a3:72-52=8×3;……
根据上述规律解决下列问题:
⑴写出第a4个等式:___________;
⑵写出你猜想的第an个等式(用含n的式子表示),并验证其正确性;
科目:初中数学 来源: 题型:
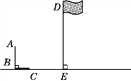
【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形![]() 位似,位似比
位似,位似比![]() =2,四边形A′B′C′D′和四边形
=2,四边形A′B′C′D′和四边形![]() 位似,位似比
位似,位似比![]() =1.四边形
=1.四边形![]() 和四边形ABCD是位似图形吗?位似比是多少?
和四边形ABCD是位似图形吗?位似比是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读材料,再尝试解决问题:
完全平方式![]() 以及
以及![]() 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求![]() 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:
解:原式 = ![]() .
.
因为无论![]() 取什么数,都有
取什么数,都有![]() 的值为非负数,所以
的值为非负数,所以![]() 的最小值为0;此时
的最小值为0;此时![]() 时,进而
时,进而![]() 的最小值是
的最小值是![]() ;所以当
;所以当![]() 时,原多项式的最小值是
时,原多项式的最小值是![]() .
.
请根据上面的解题思路,探求:
⑴.多项式![]() 的最小值是多少,并写出对应的
的最小值是多少,并写出对应的![]() 的取值;
的取值;
⑵.多项式![]() 的最大值是多少,并写出对应的
的最大值是多少,并写出对应的![]() 的取值.
的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,![]() .已知关于x,y的二元一次方程
.已知关于x,y的二元一次方程![]() (m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )

A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把正六边形对角线的交点称为它的中心,正六边形的顶点及它的中心称作特征点,如图(1)有六个顶点和一个中心点,因此共有7个特征点,照图(1)的方式继续排列正六边形,使得相邻两个正六边形的一边重合,这样得到图(2),图(3)…

观察以上图形得到表:
图形的名称 | 特征点的个数 |
图1 | 7 |
图2 | 12 |
… | … |
(1)第n个图形的特征点有多少个?
(2)第100个图形的特征点有多少个?
(3)第几个图形有2017个特征点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
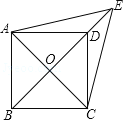
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
小明遇到这样一个问题:求计算![]() 所得多项式的一次项系数.
所得多项式的一次项系数.
小明想通过计算![]() 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
他决定从简单情况开始,先找![]() 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:
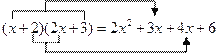
也就是说,只需用![]() 中的一次项系数1乘以
中的一次项系数1乘以![]() 中的常数项3,再用
中的常数项3,再用![]() 中的常数项2乘以
中的常数项2乘以![]() 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加![]() ,即可得到一次项系数.
,即可得到一次项系数.
延续上面的方法,求计算![]() 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用![]() 的一次项系数1,
的一次项系数1, ![]() 的常数项3,
的常数项3, ![]() 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用![]() 的一次项系数2,
的一次项系数2, ![]() 的常数项2,
的常数项2, ![]() 的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用![]() 的一次项系数3,
的一次项系数3, ![]() 的常数项2,
的常数项2, ![]() 的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
参考小明思考问题的方法,解决下列问题:
(1)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(2)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(3)若计算![]() 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则![]() =_________.
=_________.
(4)若![]() 是
是![]() 的一个因式,则
的一个因式,则![]() 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com