
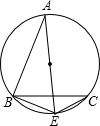
 如图,已知A为优弧中点,且AB=BC,E为劣弧
如图,已知A为优弧中点,且AB=BC,E为劣弧 上一点.
上一点. 上运动时,线段AE、BE、CE之间具有怎样的关系,画图并证明你的猜想.
上运动时,线段AE、BE、CE之间具有怎样的关系,画图并证明你的猜想. (1)证明:连接AC
(1)证明:连接AC 中点,
中点, 上则有:AE=BE-CE.
上则有:AE=BE-CE. 连接AC,
连接AC, 中点,
中点, 上则有:AE=CE-BE.证明方法一样.
上则有:AE=CE-BE.证明方法一样. 上运动时,线段AE、BE、CE之间具有的关系为:AE=|BE-CE|.
上运动时,线段AE、BE、CE之间具有的关系为:AE=|BE-CE|. 上运动时,由于△ABC为等边三角形,所以E在
上运动时,由于△ABC为等边三角形,所以E在 ,
, ,
, 上一样,图形没变,只是字母变了,所以证明的方法一样,结论形式一样,改变字母即可.不过要把E在
上一样,图形没变,只是字母变了,所以证明的方法一样,结论形式一样,改变字母即可.不过要把E在 ,
, 上的结论合起来.
上的结论合起来.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 |
| AB |
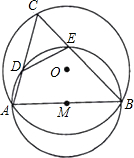 点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2
点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2| 3 |
| AD |
| DC |
查看答案和解析>>
科目:初中数学 来源: 题型:
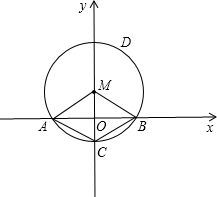 如图,已知⊙M的半径为2cm,圆心角∠AMB=120°,并建立如图所示的直角坐标系.
如图,已知⊙M的半径为2cm,圆心角∠AMB=120°,并建立如图所示的直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
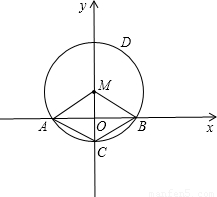
 如图,已知⊙M的半径为2cm,圆心角∠AMB=120°,并建立如图所示的直角坐标系.
如图,已知⊙M的半径为2cm,圆心角∠AMB=120°,并建立如图所示的直角坐标系.查看答案和解析>>
科目:初中数学 来源:2009年初中毕业生直升高中一年级生考试数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com