
 如图,MN是圆柱底面的直径,MP是圆柱的高,在圆柱的侧面上,过点M,P有一条绕了四周的路径最短的金属丝,现将圆柱侧面沿MP剪开,所得的侧面展开图可以是( )
如图,MN是圆柱底面的直径,MP是圆柱的高,在圆柱的侧面上,过点M,P有一条绕了四周的路径最短的金属丝,现将圆柱侧面沿MP剪开,所得的侧面展开图可以是( )| A. |  | B. | 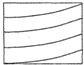 | C. |  | D. | 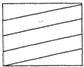 |
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:选择题
 如图,已知∠1=∠2,有下列结论:①∠3=∠D;②AB∥CD;③AD∥BC;④∠A+∠D=180°,其中正确的个数为( )
如图,已知∠1=∠2,有下列结论:①∠3=∠D;②AB∥CD;③AD∥BC;④∠A+∠D=180°,其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD.若△ABC的周长是17cm,AE=2cm,则△ABD的周长是( )
如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD.若△ABC的周长是17cm,AE=2cm,则△ABD的周长是( )| A. | 13cm | B. | 15cm | C. | 17cm | D. | 19cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}$(x-m)2+$\frac{1}{4}$m2-m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}$(x-m)2+$\frac{1}{4}$m2-m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:判断题
已知二次函数y=x2-2x-3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)求点A、B、C、D的坐标.
(2)说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到?
(3)求四边形OCDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
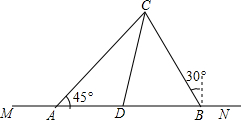 小明与小红分别住在东西大街相距10(1+$\sqrt{3}$)km的点A与点B处.在小明家北偏东45°与小红家北偏西30°的方向有两条公路交于点C,在点C的南偏西15°的方向上,且在点A与点B之间有一个以点D为圆心的方圆5km的大型批发市场.
小明与小红分别住在东西大街相距10(1+$\sqrt{3}$)km的点A与点B处.在小明家北偏东45°与小红家北偏西30°的方向有两条公路交于点C,在点C的南偏西15°的方向上,且在点A与点B之间有一个以点D为圆心的方圆5km的大型批发市场.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小王骑车从甲地到乙地,小李骑车从乙地到甲地,两人同时出发,沿同一条公路匀速前进,在出发2h时,两人相距36km,在出发3h时,两人相遇.设骑行的时间为x(h),两人之间的距离为y(km),图中的线段AB表示两人从出发到相遇这个过程中,y与x之间的函数关系.
小王骑车从甲地到乙地,小李骑车从乙地到甲地,两人同时出发,沿同一条公路匀速前进,在出发2h时,两人相距36km,在出发3h时,两人相遇.设骑行的时间为x(h),两人之间的距离为y(km),图中的线段AB表示两人从出发到相遇这个过程中,y与x之间的函数关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com