
分析 (1)根据题意设骑行队伍速度为xkm/h,则班长的速度是1.5xkm/h,再利用班长提前10分钟返回学校,得出等式求出答案;
(2)根据题意设骑行队伍速度为ykm/h,则班长的速度是aykm/h,再利用班长提前t分钟返回学校,得出等式求出答案.
解答 解:(1)设骑行队伍速度为xkm/h,则班长的速度是1.5xkm/h,根据题意可得:
$\frac{12}{x}$=$\frac{12}{1.5x}$+$\frac{10}{60}$,
解得:x=24,
经检验得:x=24是原方程的根,且有意义,
则1.5x=36(km/h),
答:骑行队伍速度为24km/h,班长的速度是36km/h;
(2)设骑行队伍速度为ykm/h,则班长的速度是aykm/h,根据题意可得:
$\frac{12}{y}$=$\frac{12}{ay}$+$\frac{t}{60}$,
解得:y=$\frac{720a-720}{ta}$,
经检验得:y=$\frac{720a-720}{ta}$是原方程的根,
则$\frac{720a-720}{ta}$•a=$\frac{720a-720}{t}$,
答:骑行队伍速度为$\frac{720a-720}{ta}$km/h,则班长的速度是$\frac{720a-720}{t}$km/h.
点评 此题主要考查了分式方程的应用,正确得出等量关系是解题关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
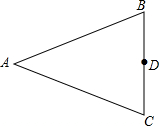 如图,在△ABC中,AB=AC,D是BC上的任意一点.
如图,在△ABC中,AB=AC,D是BC上的任意一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
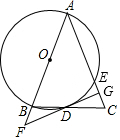 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,交AC于点E,过点D作DG⊥AC于点G,交AB的延长线于点F
如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,交AC于点E,过点D作DG⊥AC于点G,交AB的延长线于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
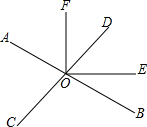 如图,两直线AB、CD相交于点O,OE平分∠BOD,如果∠AOC:∠AOD=7:11,
如图,两直线AB、CD相交于点O,OE平分∠BOD,如果∠AOC:∠AOD=7:11,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com