
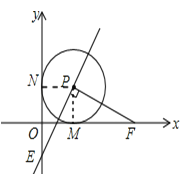
����Ŀ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬��P��1��1��ΪԲ�ĵ���P��x�ᡢy��ֱ������ڵ�M�͵�N����F�ӵ�M��������x����������ÿ��1����λ���ȵ��ٶ��˶�������PF������P��PE��PF��y���ڵ�E�����F�˶���ʱ����t�루t��0��
��1������E��y��ĸ������ϣ���ͼ��ʾ������֤��PE=PF��
��2���ڵ�F�˶������У���OE=a��OF=b�����ú�a�Ĵ���ʽ��ʾb��
��3������F���ڵ�M�ĶԳƵ�F��������M��E��F������������ߵĶԳ��ύx���ڵ�Q������QE���ڵ�F�˶������У��Ƿ����ijһʱ�̣�ʹ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�

���𰸡�(1)��֤�����̼�������(2)��b=2+a��b=2��a��(3)��t=![]() ��t=
��t=![]() ��t=2��
��t=2��![]()
�����������������(1)������PM��PN���������ߵ����ʵó�PM=PN�����ݾ�NPM=��EPF=90���ó���NPE=��MPF���Ӷ�˵����PMF����PNEȫ�ȣ��Ӷ�˵��PE=PF��(2)������t��1��1��t��1����������a��b�Ĺ�ϵ��(3)���������������εļ��ֲ�ͬ��������t��ֵ.
���������(1)����ͼ������PM��PN��
�ߡ�P��x�ᣬy��ֱ������ڵ�M�͵�N�� ��PM��MF��PN��ON��PM=PN��
���PMF=��PNE=90������NPM=90������PE��PF�� ��NPE=��MPF=90�㩁��MPE��
����PMF����PNE�У���NPE=��MPF PN=PM ��PNE=��PMF �����PMF�ա�PNE��ASA�� ��PE=PF��
(2)���⣺����t��1ʱ����E��y��ĸ������ϣ�
�ɣ�1������PMF�ա�PNE����NE=MF=t��PM=PN=1�� ��b=OF=OM+MF=1+t��a=NE��ON=t��1��
��b��a=1+t����t��1��=2����b=2+a��
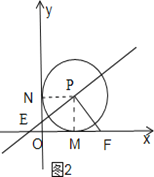
��0��t��1ʱ����ͼ2����E��y����������ԭ���ϣ�
ͬ����֤��PMF�ա�PNE�� ��b=OF=OM+MF=1+t��a=ON��NE=1��t�� ��b+a=1+t+1��t=2�� ��b=2��a��
(3)��t=![]() ��t=
��t=![]() ��t=2��
��t=2��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���ǡ�DCG=��A����E��F�ֱ��DZ�AD��BC�ϵ����㣬��EF��AB����D���1�����Ϊʲô�� 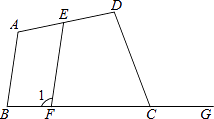
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P�ǵڶ������ڵĵ㣬�ҵ�P��x��ľ�����4����y��ľ�����3�����P�������ǣ� ��
A.����4��3��
B.��4����3��
C.����3��4��
D.��3����4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
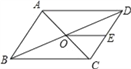
����Ŀ����ͼ, ![]() ���ܳ�Ϊ36���Խ���AC��BD�ཻ�ڵ�O����E��CD���е�,BD=12�����DOE���ܳ���
���ܳ�Ϊ36���Խ���AC��BD�ཻ�ڵ�O����E��CD���е�,BD=12�����DOE���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����A��B�����ͺż�������A�ͺż������Ľ����۸�Ϊÿ̨30Ԫ��B�ͺż������Ľ����۸�Ϊÿ̨40Ԫ���̳�����5̨A�ͺź�1̨B�ͺż��������ɻ�����76Ԫ������6̨A�ͺź�3̨B�ͺż��������ɻ�����120Ԫ��
��1���ֱ����̳�����A��B�����ͺż�����ÿ̨�����ۼ۸�
��2���̳����ò�����2 500Ԫ���ʽ�A��B�����ͺż�������70̨����������Ҫ����A�ͺŵļ���������̨��������=���ۼ۸����۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a�����ĸ�������b����С����������c�Ǿ���ֵ��С��������(a��c)��b��___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BOC=9�㣬��A��OB�ϣ���OA=1��������Ҫ��ͼ��
��AΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A1���õ�1���߶�AA1������A1ΪԲ�ģ�1Ϊ�뾶���һ�����OB�ڵ�A2���õ�2���߶�A1A2������A2ΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A3���õ�3���߶�A2A3������������ȥ��ֱ���õ�n���߶Σ�֮��Ͳ����ٻ�������Ҫ����߶��ˣ���n=______��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com