
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.正确结论有( )

A. 4个B. 3个C. 2个D. 1个
【答案】B
【解析】
根据同角的余角相等求出∠BAD=∠C,再根据等角的余角相等可以求出∠AEF=∠AFE;根据等腰三角形三线合一的性质求出AG⊥EF.
∵∠BAC=90°,AD⊥BC,
∴∠C+∠ABC=90°,
∠BAD+∠ABC=90°,
∴∠BAD=∠C,故①正确;
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,
∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
又∵∠AFE=∠BFD(对顶角相等),
∴∠AEF=∠AFE,故②正确;
∵∠ABE=∠CBE,
∴只有∠C=30°时∠EBC=∠C,故③错误;
∵∠AEF=∠AFE,
∴AE=AF,
∵AG平分∠DAC,
∴AG⊥EF,故④正确.
综上所述,正确的结论是①②④.
故选B.


科目:初中数学 来源: 题型:
【题目】甲、乙两人分别骑自行车和摩托车,从同一地点沿相同的路线前往距离80km的某地,图中l1,l2分别表示甲、乙两人离开出发地的距离s(km)与行驶时间t(h)之间的函数关系.请根据图象解答下列问题:
(1)甲、乙两人谁到达目的地较早?早多长时间?
(2)分别求甲、乙两人行驶过程中s与t的函数关系式;
(3)试确定当两辆车都在行驶途中(不包括出发地和目的地)时,t的取值范围;并在这一时间段内,求t为何值时,摩托车行驶在自行车前面?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,长方形ABCD的边BC平行于x轴,如果点A的坐标为(-1,2),点C的坐标为(3,-3),把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按如图所示的逆时针方向绕在长方形ABCD的边上,则细线的另一端所在位置的点的坐标是( )

A. (-1,1)B. (-1,-1)C. (2,-2)D. (2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.
(1)试探究BE与BF的数量关系,并证明你的结论;
(2)求EF的最大值与最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1中ΔABC是等边三角形,DE是中位线,F是线段BC延长线上一点,且CF=AE,连接BE,EF.
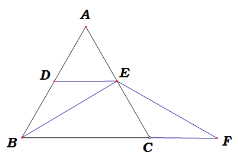

图1 图2
(1)求证:BE=EF;
(2)若将DE从中位线的位置向上平移,使点D、E分别在线段AB、AC上(点E与点A不重合),其他条件不变,如图2,则(1)题中的结论是否成立?若成立,请证明;若不成立.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
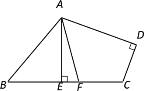
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,∠A=x°,∠C=y°(0°<x<180°,0°<y<180°).
(1)∠ABC+∠ADC= °.(用含x,y的代数式表示)
(2)如图1,若x=y=90°,DE平分∠ADC,BF平分与∠ABC相邻的外角,请写出DE与BF的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角,
①当x<y时,若x+y=140°,∠DFB=30°,试求x、y.
②小明在作图时,发现∠DFB不一定存在,请直接指出x、y满足什么条件时,∠DFB不存在.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=______s时,以A、C、E、F为顶点四边形是平行四边形.
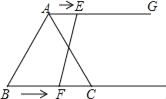
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com