
 某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°,则调整后楼梯AD的长为6$\sqrt{2}$m.(结果保留根号)
某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°,则调整后楼梯AD的长为6$\sqrt{2}$m.(结果保留根号) 科目:初中数学 来源: 题型:填空题
 如图所示的圆柱体中底面圆的半径是$\frac{4}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是4$\sqrt{2}$.
如图所示的圆柱体中底面圆的半径是$\frac{4}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
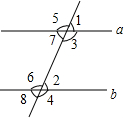 如图,在条件:①∠5=∠6,②∠7=∠2,③∠3+∠8=180°,④∠3=∠2,⑤∠4+∠1=180°中,能判定a∥b的条件有( )
如图,在条件:①∠5=∠6,②∠7=∠2,③∠3+∠8=180°,④∠3=∠2,⑤∠4+∠1=180°中,能判定a∥b的条件有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com