
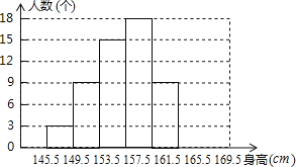
”¾ĢāÄæ”æ ĪŖĮĖ½ā¾ÅÄź¼¶Å®ÉśµÄÉķøߣص„Ī»£ŗcm£©Ēéæö£¬Ä³ÖŠŃ§¶Ō²æ·Ö¾ÅÄź¼¶Å®ÉśÉķøß½ųŠŠĮĖŅ»“Ī²āĮ棬ĖłµĆŹż¾ŻÕūĄķŗóĮŠ³öĮĖʵŹż·Ö²¼±ķ£¬²¢»ĮĖ²æ·ÖʵŹż·Ö²¼Ö±·½Ķ¼£ØĶ¼”¢±ķČēĶ¼£©£ŗ
·Ö×é | ʵŹż | ʵĀŹ |
145.5-149.5 | 3 | 0.05 |
149.5-153.5 | 9 | n |
153.5-157.5 | m | 0.25 |
157.5-161.5 | 18 | 0.30 |
161.5-165.5 | 9 | 0.15 |
165.5-169.5 | 6 | 0.10 |
ŗĻ¼Ę | M | N |
øł¾ŻŅŌÉĻĶ¼±ķ£¬»Ų“šĪŹĢā£®
£Ø1£©M=______£¬m=______£¬N=______£¬n=______£»
£Ø2£©²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼£»
£Ø3£©Čō¾ÅÄź¼¶ÓŠ600Ćūѧɜ£¬ŌņÉķøßŌŚ161.5-165.5·¶Ī§Ō¼ĪŖ¶ąÉŁČĖ£æ
”¾“š°ø”æ£Ø1£©60£¬15£¬1£¬0.15£»£Ø2£©Ļź¼ū½āĪö£»£Ø3£©90
”¾½āĪö”æ
£Ø1£©øł¾ŻµŚŅ»×éµÄʵŹżŹĒ3£¬ĘµĀŹŹĒ0.05£¬ŅĄ¾ŻĘµĀŹ=![]() £¬¼“æÉĒóµĆ×ÜŹżMµÄÖµ£¬Č»ŗóĄūÓĆ¹«Ź½¼“æÉĒóµĆm”¢nµÄÖµ£»
£¬¼“æÉĒóµĆ×ÜŹżMµÄÖµ£¬Č»ŗóĄūÓĆ¹«Ź½¼“æÉĒóµĆm”¢nµÄÖµ£»
£Ø2£©øł¾Ż£Ø1£©ÖŠmµÄÖµ¼“æÉ×÷³öĶ³¼ĘĶ¼£»
£Ø3£©ĄūÓĆ600³ĖŅŌÉķøßŌŚ161.5-165.5·¶Ī§µÄʵĀŹ¼“æÉĒó½ā£®
½ā£ŗ£Ø1£©M=3”Ā0.05=60£¬m=60”Į0.25=15£¬N=1£¬n=![]() =0.15£»
=0.15£»
¹Ź“š°øĪŖ£ŗ60£¬15£¬1£¬0.15£»
£Ø2£©²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼ČēĶ¼ĖłŹ¾£»
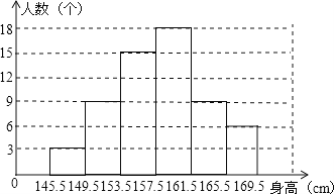
£Ø3£©600”Į0.15=90(ČĖ)
“š£ŗÉķøßŌŚ161.5-165.5·¶Ī§Ō¼ĪŖ90ČĖ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() Ę½·Ö
Ę½·Ö![]() £¬
£¬![]() £¬
£¬![]() £¬ÄĒĆ“
£¬ÄĒĆ“![]() µÄ³¤ŹĒ ____________£®
µÄ³¤ŹĒ ____________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø3·Ö£©ŅŌĻĀĖÄÖÖŃŲABÕŪµžµÄ·½·ØÖŠ£¬²»Ņ»¶ØÄÜÅŠ¶ØÖ½“ųĮ½Ģõ±ßĻßa£¬b»„ĻąĘ½ŠŠµÄŹĒ£Ø £©
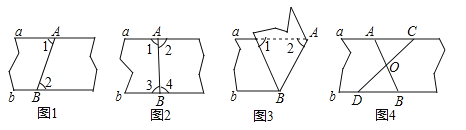
A. ČēĶ¼1£¬Õ¹æŖŗó²āµĆ”Ļ1=”Ļ2
B. ČēĶ¼2£¬Õ¹æŖŗó²āµĆ”Ļ1=”Ļ2ĒŅ”Ļ3=”Ļ4
C. ČēĶ¼3£¬²āµĆ”Ļ1=”Ļ2
D. ČēĶ¼4£¬Õ¹æŖŗóŌŁŃŲCDÕŪµž£¬Į½ĢõÕŪŗŪµÄ½»µćĪŖO£¬²āµĆOA=OB£¬OC=OD
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹż![]() µÄĶ¼ĻńÓė
µÄĶ¼ĻńÓė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬Ņ»“ĪŗÆŹż
£¬Ņ»“ĪŗÆŹż![]() µÄĶ¼Ļń¹żµć
µÄĶ¼Ļń¹żµć![]() £¬ĒŅÓė
£¬ĒŅÓė![]() Öį¼°
Öį¼°![]() µÄĶ¼Ļń·Ö±š½»ÓŚµć
µÄĶ¼Ļń·Ö±š½»ÓŚµć![]() ”¢
”¢![]() £¬
£¬![]() µć×ų±źĪŖ
µć×ų±źĪŖ![]() .
.
£Ø1£©ĒónµÄÖµ¼°Ņ»“ĪŗÆŹż![]() µÄ½āĪöŹ½.
µÄ½āĪöŹ½.
£Ø2£©ĒóĖıߊĪ![]() µÄĆ껿.
µÄĆ껿.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ ŅŌĻĀŃŲABÕŪµžµÄ·½·ØÖŠ£¬²»Ņ»¶ØÄÜÅŠ¶ØÖ½“ųĮ½Ģõ±ßa£¬b»„ĻąĘ½ŠŠµÄŹĒ£Ø””””£©
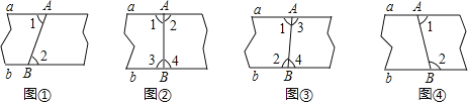
A.ČēĶ¼¢Ł£¬Õ¹æŖŗó²āµĆ”Ļ1=”Ļ2B.ČēĶ¼¢Ś£¬Õ¹æŖŗó²āµĆ”Ļ1=”Ļ2£¬ĒŅ”Ļ3=”Ļ4
C.ČēĶ¼¢Ū£¬Õ¹æŖŗó²āµĆ”Ļ1=”Ļ2£¬ĒŅ”Ļ3=”Ļ4D.ČēĶ¼¢Ü£¬Õ¹æŖŗó²āµĆ”Ļ1+”Ļ2=180”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠµÄµćP£Øa£¬b£©£¬ČōµćP”äµÄ×ų±źĪŖ£Øa+kb£¬ka+b£©£ØĘäÖŠkĪŖ³£Źż£¬ĒŅk”Ł0£©£¬
Ōņ³ĘµćP”äĪŖµćPµÄ”°kŹōÅÉÉśµć”±£®ĄżČē£ŗP£Ø1£¬4£©µÄ”°2ŹōÅÉÉśµć”±ĪŖP”ä£Ø1+2”Į4£¬2”Į1+4£©£¬¼“P”ä£Ø9£¬6£©£®
£Ø¢ń£©µćP£Ø©2£¬3£©µÄ”°3ŹōÅÉÉśµć”±P”äµÄ×ų±źĪŖ”” ””£»
£Ø¢ņ£©ČōµćPµÄ”°5ŹōÅÉÉśµć”±P”äµÄ×ų±źĪŖ£Ø3£¬©9£©£¬ĒóµćPµÄ×ų±ź£»
£Ø¢ó£©ČōµćPŌŚxÖįµÄÕż°ėÖįÉĻ£¬µćPµÄ”°kŹōÅÉÉśµć”±ĪŖP”äµć£¬ĒŅĻ߶ĪPP”äµÄ³¤¶ČĪŖĻ߶ĪOP³¤¶ČµÄ2±¶£¬ĒókµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
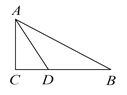
”¾ĢāÄæ”æČēĶ¼£¬”ĻCAB=”ĻDBA£¬ŌŁĢķ¼ÓŅ»øöĢõ¼ž£¬²»Ņ»¶ØÄÜÅŠ¶Ø”÷ABC”Õ”÷BADµÄŹĒ£Ø””””£©
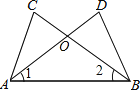
A. AC=BDB. ”Ļ1=”Ļ2C. AD=BCD. ”ĻC=”ĻD
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬µćOŹĒµČ±ßČż½ĒŠĪABCÄŚŅ»µć£¬”ĻAOB=110”ć£¬”ĻBOC=¦Į, ŅŌOCĪŖ±ß×÷µČ±ßČż½ĒŠĪOCD£¬Į¬½ÓAD.

£Ø1£©µ±¦Į=150”揱£¬ŹŌÅŠ¶Ļ”÷AODµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©Ģ½¾æ£ŗµ±aĪŖ¶ąÉŁ¶ČŹ±£¬”÷AODŹĒµČŃüČż½ĒŠĪ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij°ą½«ĀņŅ»Š©Ę¹ÅŅĒņŗĶĘ¹ÅŅĒņÅÄ£¬ĻÖĮĖ½āĒéæöČēĻĀ£ŗ¼×ŅŅĮ½¼ŅÉĢµź³öŹŪĮ½ÖÖĶ¬ŃłĘ·ÅʵÄĘ¹ÅŅĒņŗĶĘ¹ÅŅĒņÅÄ£¬Ę¹ÅŅĒņÅÄĆæø±¶Ø¼Ū30ŌŖ£¬Ę¹ÅŅĒņĆæŗŠ¶Ø¼Ū5ŌŖ£¬¾Ē¢Ģøŗ󣬼׵źĆæĀņŅ»ø±ĒņÅÄŌłŅ»ŗŠĘ¹ÅŅĒņ£¬ŅŅµźČ«²æ°“¶Ø¼ŪµÄ9ÕŪÓÅ»Ż£¬øĆ°ąĻÖŠčĒņÅÄ5ø±£¬Ę¹ÅŅĒņČōøÉŗŠ(²»Š”ÓŚ5ŗŠ)£®ĪŹ£ŗ
(1)Čō¹ŗĀņµÄĘ¹ÅŅĒņĪŖ![]() ŗŠ£¬Ēė·Ö±šÓĆ“śŹżŹ½±ķŹ¾ŌŚĮ½¼Ņµź¹ŗĀņÕāŠ©Ę¹ÅŅĒņŗĶĘ¹ÅŅĒņÅÄŹ±Ó¦øĆÖ§ø¶µÄ·ŃÓĆ£»
ŗŠ£¬Ēė·Ö±šÓĆ“śŹżŹ½±ķŹ¾ŌŚĮ½¼Ņµź¹ŗĀņÕāŠ©Ę¹ÅŅĒņŗĶĘ¹ÅŅĒņÅÄŹ±Ó¦øĆÖ§ø¶µÄ·ŃÓĆ£»
(2)µ±¹ŗĀņ15ŗŠ”¢30ŗŠĘ¹ÅŅĒņŹ±£¬ĒėÄćČ„°ģÕā¼žŹĀ£¬Äć“ņĖćČ„ÄļŅÉĢµź¹ŗĀņ£¬ĪŖŹ²Ć“£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com