
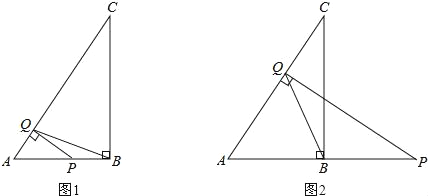
【题目】在△ABC中,∠ABC=90°,已知AB=3,BC=4,点Q是线段AC上的一个动点,过点Q作AC的垂线交直线AB于点P,当△PQB为等腰三角形时,线段AP的长为 .
【答案】![]() 或6.
或6.
【解析】试题解析:(2)在Rt△ABC中,AB=3,BC=4,由勾股定理得:AC=5.
∵∠QPB为钝角,
∴当△PQB为等腰三角形时,
(I)当点P在线段AB上时,如题图1所示:
∵∠QPB为钝角,
∴当△PQB为等腰三角形时,只可能是PB=PQ,
由(1)可知,△AQP∽△ABC,
∴![]() 即
即![]() 解得:
解得: ![]()
∴![]()
(II)当点P在线段AB的延长线上时,如题图2所示:
∵∠QBP为钝角,
∴当△PQB为等腰三角形时,只可能是PB=BQ.
∵BP=BQ,∴∠BQP=∠P,
∵![]()
∴∠AQB=∠A,
∴BQ=AB,
∴AB=BP,点B为线段AP中点,
∴AP=2AB=2×3=6.
综上所述,当△PQB为等腰三角形时,AP的长为![]() 或6.
或6.
故答案为: ![]() 或6.
或6.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
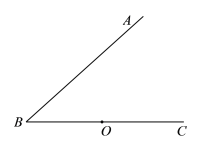
【题目】如图,点O为∠ABC的边![]() 上的一点,过点O作OM⊥AB于点
上的一点,过点O作OM⊥AB于点![]() ,到点
,到点![]() 的距离等于线段OM的长的所有点组成图形
的距离等于线段OM的长的所有点组成图形![]() .图形W与射线
.图形W与射线![]() 交于E,F两点(点在点F的左侧).
交于E,F两点(点在点F的左侧).
(1)过点![]() 作
作![]() 于点
于点![]() ,如果BE=2,
,如果BE=2,![]() ,求MH的长;
,求MH的长;
(2)将射线BC绕点B顺时针旋转得到射线BD,使得∠![]()
![]() ,判断射线BD与图形
,判断射线BD与图形![]() 公共点的个数,并证明.
公共点的个数,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
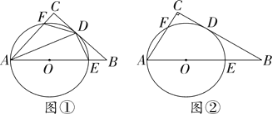
【题目】在△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为弧AD的中点,⊙O的半径为2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:若关于x的一元二次方程ax2+bx+c=0的两个非零实数根分别为x1,x2,则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() .
.
解决下列问题:已知关于x的一元二次方程(x+n)2=6x有两个非零不等实数根x1,x2,设m=![]() ,
,
(Ⅰ)当n=1时,求m的值;
(Ⅱ)是否存在这样的n值,使m的值等于![]() ?若存在,求出所有满足条件的n的值;若不存在,请说明理由.
?若存在,求出所有满足条件的n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为弧AD的中点,连接CE交AB于点F,且BF=BC.

(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,![]() =
=![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
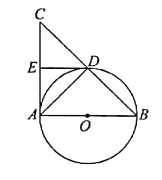
【题目】如图,点![]() 是
是![]() 中
中![]() 边的中点,
边的中点,![]() 于
于![]() ,以
,以![]() 为直径的
为直径的![]() 经过
经过![]() ,连接
,连接![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是
是![]() 的切线.其中正确的结论是( )
的切线.其中正确的结论是( )
A.①②B.①②③C.②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() ,其顶点为A.
,其顶点为A.
(1)写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;
(2)直线BC平行于x轴,交这条抛物线于B、C两点(点B在点C左侧),且![]() ,求点B坐标.
,求点B坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
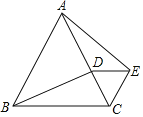
【题目】如图,△ABC是等边三角形,点D在AC边上,将△BCD绕点C旋转得到△ACE.
(1)求证:DE∥BC.
(2)若AB=8,BD=7,求△ADE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com