
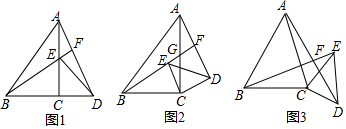
分析 (2)①只要证明△BCE≌△ACD写出理由,即可解决问题;
②利用“8字型”证明∠AFG=∠BCG即可解决问题;
(3)①只要证明△BCE≌△ACD写出理由,即可解决问题;
②利用“8字型”证明∠AFG=∠BCG即可解决问题;
解答 (2)证明:①∵∠ACB=∠DCE=90°(已知),∠ACB=∠BCE+∠ACE,∠ECD=∠ACD+∠ACE
∴∠BCE=∠ACD(同角的余角相等)
又∵BC=AC,CE=CD(已知),
∴△BCE≌△ACD( SAS)
∴BE=AD( 全等三角形对应边相等)
②由①得,∠CBE=∠CAD(全等三角形的对应角相等),
∵∠CBE+∠CGB=90°(直角三角形的两个锐角互余),
∠CGB=∠AGF( 对顶角相等)
∴∠CAD+∠AGF=90°(等量代换)
∵∠AGF+∠CAD+∠AFE=180°(三角形内角和定理),
∴∠AFE=90°.
故答案为∠BCE=∠ACD,全等三角形对应边相等,全等三角形的对应角相等,对顶角相等,三角形内角和定理.
(3):①设AC交BE于G,
∵∠ACB=∠DCE=70°,
∴∠BCE=∠ACD,
又∵BC=AC,CE=CD(已知),
∴△BCE≌△ACD( SAS),
∴BE=AD( 全等三角形对应边相等),
②由①得,∠CBE=∠CAD(全等三角形的对应角相等),
∵∠CGB=∠AGF( 对顶角相等),
∴∠BCG=∠AFG=70°,
∴∠AFE=180°-70°=110°.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、三角形内角和定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
 如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点.
如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 59 | 96 | 116 | 295 | 480 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com