
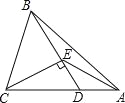
【题目】如图,△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.
求证:(1)DE=DA;(2)CE2=ADAC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据直角三角形30度角性质得到DE=![]() CD,根据已知条件AD=
CD,根据已知条件AD=![]() DC,由此不难证明.
DC,由此不难证明.
(2)先证明∠ECA=∠EAC=∠AED=30°,再证明△DEA∽△ECA即可.
试题解析:(1)∵CE⊥BD,∠BDC=60°
∴∠ECD=30°,
∴DE=![]() CD,又∵CD=2DA,即DA=
CD,又∵CD=2DA,即DA=![]() CD,
CD,
∴ED=DA.
(2)∵∠EDC=60°=∠DEA+∠DAE,
∵DE=DA,
∴∠DEA=∠DAE=30°,
∵∠ECD=30°,
∴∠ECA=∠EAC=∠AED=30°,
∴EC=EA,
∵∠EAD=∠CAE,∠AED=∠ACE
∴△DEA∽△ECA,
∴![]() ,
,
∴AE2=ADAC,∴EA=EC,
∴EC2=ADAC.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】若y轴上的点A到x轴的距离为3,则点A的坐标为( )
A. (3,0) B. (3,0)或(-3,0)
C. (0,3) D. (0,3)或(0,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=![]() (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
(1)求反比例函数的表达式.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
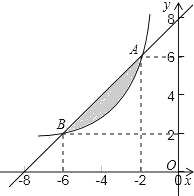
【题目】如图A、B两点在函数y=![]() (x<0)的图象上.
(x<0)的图象上.
(1)求k的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点叫做格点,请直接写出图中阴影部分(含边界)所含格点的坐标(A、B两点除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是一元二次方程x2+mx-1=0的两个实数根,x1<x2; x3,x4是一元二次方程x2+mx-2=0的两个实数根, x3<x4 .则下列结论正确的是( )
A. x1<x2< x3<x4 B. x1 < x3<x4 <x2 C. x3< x1<x2<x4 D. x1 < x3<x2<x4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( ).
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事实可以用“两点确定一条直线”来解释的个数为
①墙上钉木条至少要两颗钉子才能牢固;②农民拉绳播秧;③解放军叔叔打靶瞄准;④从A地到B地架设电线,总是尽可能沿着线段AB架设.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com