若kb＞0.且不等式kx+b＞0的解集是x＜-$\frac{b}{k}$.则下列判断正确的是( )A．k＞0.b＞0B．k＞0.b＜0C．k＜0.b＜0D．k＜0.b＞0 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

2．若kb＞0，且不等式kx+b＞0的解集是x＜-$\frac{b}{k}$，则下列判断正确的是（　　）

A．

k＞0，b＞0

B．

k＞0，b＜0

C．

k＜0，b＜0

D．

k＜0，b＞0

分析首先根据不等式kx+b＞0的解集是x＜-$\frac{b}{k}$，应用不等式的性质，可得k＜0；然后根据kb＞0，可得b＜0，据此解答即可．

解答解：∵不等式kx+b＞0的解集是x＜-$\frac{b}{k}$，
∴k＜0，
又∵kb＞0，
∴b＜0，
综上，可得k＜0，b＜0．
故选：C．

点评此题主要考查了不等式的解集问题，要熟练掌握，解答此题的关键是根据不等式的性质，判断出k＜0．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

12．

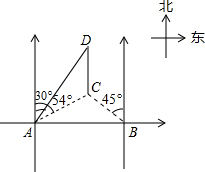如图，在海岸边相距12km的两个观测站A、B，同时观测到一货船C的方向角分别为北偏东54°和北偏西45°，该货船向正北航行，与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物，正好在D处追上货船，求快艇追赶的时间．（参考数据：sin54°≈0.8，cos54°≈0.6，tan54°≈1.4）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

13．

如图，AB是⊙O的直径，AD是⊙O的切线，BC∥OD交⊙O于点C，若AB=2，OD=3，则BC的长为（　　）

A．

$\frac{3}{2}$

B．

$\frac{2}{3}$

C．

$\frac{{\sqrt{3}}}{2}$

D．

$\frac{{\sqrt{2}}}{2}$

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

10．一个布袋中有5个除颜色外其余都相同的小球，其中3个白球，2个红球．从袋中任意摸出1个球是白球的概率是$\frac{3}{5}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．如图，已知抛物线y=ax²+bx+c经过点A（-1，0）、B（3，0）、C（0，3）三点．
（1）求抛物线相应的函数表达式；
（2）点M是线段BC上的点（不与B、C重合），过M作MN∥y轴交抛物线于N，连接NB．若点M的横坐标为t，是否存在t，使MN的长最大？若存在，求出sin∠MBN的值；若不存在，请说明理由；
（3）若对一切x≥0均有ax²+bx+c≤mx-m+13成立，求实数m的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．

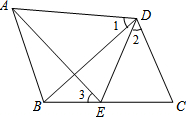已知：如图，AD=BD，CD=ED，∠1=∠2，试说明∠3=∠1的理由．
解：因为∠1=∠2（已知），
所以∠1+∠BDE=∠2+∠BDE（等式性质），
即∠ADE=∠BDC．
在△ADE和△BDC中，
$\left\{\begin{array}{l}{AD=BD（已知）}\\{∠（）=∠（）}\\{ED=CD（已知）}\end{array}\right.$所以△ADE≌△BDC（SAS）．
所以∠AED=∠C（全等三角形对应角相等）．
又因为∠BED=∠2+∠C（三角形的一个外角等于与它不相邻的两个内角的和），
即∠3+∠AED=∠2+∠C，
所以∠3=∠2（等式的性质）．
因为∠1=∠2（已知），
所以∠3=∠1（等量代换）．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

14．

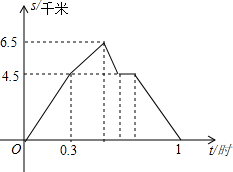从A到B地的一条公路，先是一段平路，然后是一段上坡路，小明骑自行车从A地出发，到达B地后立即按原路返回A地，返回途中休息了一段时间，假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进．已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米．下坡路的速度比在平路上的速度每小时多5千米，小明在去B地和返回A地两次经过C地的时间间隔为0.15小时，小明离A地的路程S（单位：千米）和出发的时间t（单位：小时）之间的函数关系式如图所示．下列说法中正确的个数为（　　）
①小明骑自行车在上坡路的速度为10千米/时；
②小明从A地到B地共用了0.4小时；
③小明在返回途中休息了0.1小时；
④C地与B地的距离为1千米．

A．

1个

B．

2个

C．

3个

D．

4个

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

11．

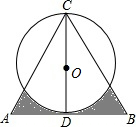如图，△ABC是边长为4的等边三角形，D为AB边的中点，以CD为直径画圆，则图中阴影部分的面积为2.5$\sqrt{3}$-π（结果保留π）．