
【题目】为了落实党的“精准扶贫”政策,A,B两城决定向C,D两乡运送肥料以支持农村生产.已知A,B两城分别有肥料210吨和290吨,从A城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)设从A城运往C乡肥料x吨.
①用含x的代数式完成下表:
C乡(吨) | D乡(吨) | |
A城 | x | |
B城 | ||
总计 | 240 | 260 |
②设总运费为y元,写出y与x的函数关系式,并求出最少总运费;
(2)由于更换车型,使从A城往C乡运肥料的费用每吨减少a(![]() )元,这时从A城往C乡运肥料多少吨时总运费最少?
)元,这时从A城往C乡运肥料多少吨时总运费最少?
【答案】(1)①![]()
![]()
![]() ;② y
;② y![]() ,最少运费是10050元;(2)当
,最少运费是10050元;(2)当![]() 时,0吨;当
时,0吨;当![]() 时,210吨;当
时,210吨;当![]() 时,不管A城运往C乡多少吨(不超过210吨),运费都是10050
时,不管A城运往C乡多少吨(不超过210吨),运费都是10050
【解析】
(1)①由从A城运往C乡肥料x吨,根据题意,直接写出答案即可;②根据题意,写出y与x的函数关系式,根据一次函数的增减性,即可求解;
(2)根据A城往C乡的运肥料费用每吨减少![]() 元,列出y与x的函数关系式,再分三种情况讨论:当
元,列出y与x的函数关系式,再分三种情况讨论:当![]() 时,当
时,当![]() 时, 当
时, 当![]() 时,分别求解,即可.
时,分别求解,即可.
(1)①由从A城运往C乡肥料x吨,可得从A城运往D乡的肥料为![]() 吨;
吨;
从B城运往C乡的肥料为![]() 吨,从B城运往D乡的肥料为
吨,从B城运往D乡的肥料为![]() 吨;
吨;
故答案为:![]()
![]()
![]() .
.
②![]()
![]() ,
,
∵![]() 是一次函数,且
是一次函数,且![]() ,
,
∴y随x的增大而增大.
∵![]() ,
,
∴当![]() 时,运费最少,最少运费是10050元.
时,运费最少,最少运费是10050元.
(2)从A城往C乡运肥料x吨,由于A城往C乡的运肥料费用每吨减少![]() 元,
元,
∴![]()
![]() .
.
当![]() 时,
时,![]() , y随x的增大而增大.
, y随x的增大而增大.
∴当![]() 时,运费最少,最少是10050元;
时,运费最少,最少是10050元;
当![]() 时,
时,![]() ,y随x的增大而减小,
,y随x的增大而减小,
∴当![]() 时,运费最少;
时,运费最少;
当![]() 时,不管A城运往C乡多少吨(不超过210吨),运费都是10050元.
时,不管A城运往C乡多少吨(不超过210吨),运费都是10050元.


科目:初中数学 来源: 题型:
【题目】某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收1元印刷费,另收150元的制版费;乙印刷厂提出:每份材料收2.5元印刷费,不收制版费.设在同一家印刷厂一次印制数量为![]() 份(
份(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
一次印制数量(份) | 5 | 10 | 20 | … |
|
甲印刷厂收费(元) | 155 | … | |||
乙印刷厂收费(元) | 12.5 | … |
(2)在印刷品数量大于800份的情况下选哪家印刷厂印制省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作☉O,交BD于点E,连接CE,过D作DF![]() AB于点F,∠BCD=2∠ABD.
AB于点F,∠BCD=2∠ABD.
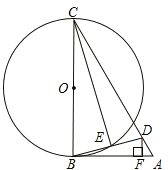
(1)求证:AB是☉O的切线;
(2)若∠A=60°,DF=![]() ,求☉O的直径BC的长。
,求☉O的直径BC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
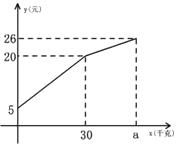
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
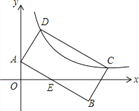
【题目】如图,矩形ABCD中,AB=2AD,点A(0,1),点C、D在反比例函数![]() (k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为_____.
(k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018中国重庆开州汉丰湖国际摩托艇公开赛第二年举办.邻近区县一旅行社去年组团观看比赛,全团共花费9600元.今年赛事宣传工作得力,该旅行社继续组团前来观看比赛,人数比去年增加了![]() ,总费用增加了3900元,人均费用反而下降了20元.
,总费用增加了3900元,人均费用反而下降了20元.
(1)求该旅行社今年有多少人前来观看赛事?
(2)今年该旅行社本次费用中,其它费用不低于交通费的2倍,求人均交通费最多为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B(3,3)在双曲线y=![]() (x>0)上,点D在双曲线
(x>0)上,点D在双曲线![]() (x<0)上,点A和点C分别在x轴,y轴的正半轴上,DM⊥x轴于M,BN⊥x轴于N,且点A、 B、 C、D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,DM⊥x轴于M,BN⊥x轴于N,且点A、 B、 C、D构成的四边形为正方形.
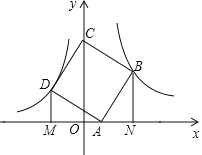
(1)k的值为___;
(2)求证:△ADM≌△BAN;
(3)求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:(一)如果我们能找到两个实数x、y使![]() 且
且![]() ,这样
,这样![]() ,那么我们就称
,那么我们就称![]() 为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.
为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.
例如:![]() .
.
(二)在进行二次根式的化简与运算时,我们有时还会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: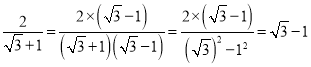 ,那么我们称这个过程为分式的分母有理化.
,那么我们称这个过程为分式的分母有理化.
根据阅读材料解决下列问题:
(1)化简“和谐二次根式”:①![]() ___________,②___________;
___________,②___________;
(2)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的小数部分为
的小数部分为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com