练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．若二次三项式4a2+（m+1）a+9可以化为完全平方的形式，则m=11或-13．

    分析 利用完全平方公式的结构特征判断即可．

    解答 解：∵二次三项式4a2+（m+1）a+9可以化为完全平方的形式，
    ∴m+1=±12，
    解得：m=11或m=-13，
    故答案为：11或-13

    点评 此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．如图，数轴上点A、B、C分别对应1、2、3，过点C作PQ⊥AB，以点C为圆心，BC长为半径画弧，交PQ于点D，以点A为圆心，AD长为半径画弧，交数轴于点M，则点M对应的数是（　　）
    A．$\sqrt{3}$+1B．$\sqrt{5}$+1C．$\sqrt{3}$D．$\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．在△ABC中，AB=AC，BD平分∠ABC，交AC于D点，若BD=BC，求∠DBC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，已知∠1+∠2=180°，∠B=∠3，试判断∠BAC和∠CED的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：
    （1）（$\frac{1}{3}$）-2-（-1）2016-$\sqrt{25}$+（π-1）0  
    （2）$\frac{x}{x-1}$-$\frac{3x-1}{{x}^{2}-1}$  
    （3）$\frac{1}{2a}$-$\frac{1}{a+b}$（$\frac{a+b}{2a}$-a-b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图 A（0，-4）、B（-2，0），M为直线l1：x=-1上一点，N为直线l2：y=x+3上一点．若以A、B、M、N为顶点的四边形是平行四边形，求所有满足条件的点N的坐标；
    点拨：平行四边形转化为点的平移或平移的全等三角形；
    认真审题，数形结合（画尽量准确的图），分类讨论（AB为边或对角线）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图①，将一张直角三角形纸片△ABC折叠，使点A与点C重合，这时DE为折痕，△CBE为等腰三角形；再继续将纸片沿△CBE的对称轴EF折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”．
    （1）如图②，正方形网格中的△ABC能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；
    （2）如图③，在正方形网格中，以给定的BC为一边，画出一个斜三角形ABC，使其顶点A在格点上且△ABC折成的“叠加矩形”为正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：
    （1）（4$\sqrt{2}$-3$\sqrt{8}$）÷2$\sqrt{2}$；
    （2）|-1|-$\sqrt{4}$+（π-3）0+2-1．

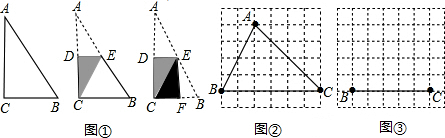
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，水平桌面上有个内部装水的长方体箱子，箱内有一个与底面垂直的隔板，且隔板左右两侧的水面高度为别为40公分，50公分，今将隔板抽出，若过程中箱内的水量未改变，且不计箱子及隔板厚度，则根据图中的数据，求隔板抽出后水面静止时，箱内的水面高度为多少公分（　　）
    A．43B．44C．45D．46

    查看答案和解析>>

    同步练习册答案